题目内容
14.关于抛物线y=x2-2x+1,下列说法错误的是( )| A. | 开口向上 | B. | 与x轴有两个重合的交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
分析 根据抛物线的解析式画出抛物线的图象,根据二次函数的性质结合二次函数的图象,逐项分析四个选项,即可得出结论.
解答 解:画出抛物线y=x2-2x+1的图象,如图所示.
A、∵a=1,
∴抛物线开口向上,A正确;
B、∵令x2-2x+1=0,△=(-2)2-4×1×1=0,
∴该抛物线与x轴有两个重合的交点,B正确;
C、∵-$\frac{b}{2a}$=-$\frac{-2}{2×1}$=1,
∴该抛物线对称轴是直线x=1,C正确;
D、∵抛物线开口向上,且抛物线的对称轴为x=1,
∴当x>1时,y随x的增大而增大,D不正确.
故选D.
点评 本题考查了二次函数的性质以及二次函数的图象,解题的关键是结合二次函数的性质及其图象分析四个选项.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的解析式画出函数图象,利用数形结合来解决问题是关键.

练习册系列答案
相关题目
4.下列四个数中最大的数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
19.-$\sqrt{2}$的相反数是( )
| A. | $\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -2 |
 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度.
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度.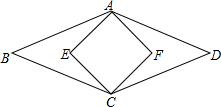 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm. 将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.
将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.