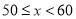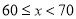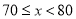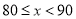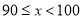题目内容
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A. 2 B. 2.5或3.5 C. 3.5或4.5 D. 2或3.5或4.5
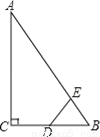
D 【解析】试题分析:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,∴AB=2BC=4(cm),∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发, ∴BD=BC=1(cm),BE=AB﹣AE=4﹣t(cm),若∠BED=90°,当A→B时,∵∠ABC=60°,∴∠BDE=30°,∴BE=BD=(cm),∴t=3.5,当B→A时,t=4+0.5=4...如图,在△ABC中, 若DE∥BC , 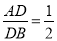 ,DE=4cm,则BC的长为 ( )
,DE=4cm,则BC的长为 ( )
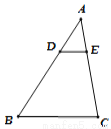
A. 8cm B. 12cm C. 11cm D. 10cm
查看答案如图,下列各式能使ΔACB∽ΔDCA的是( )
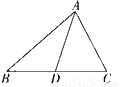
A. 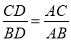 B.
B. 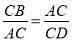 C.
C. 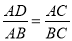 D.
D. 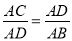
在同一平面直角坐标系中,一次函数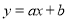
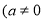 )和二次函数
)和二次函数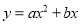
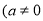 )的图象可能为( )
)的图象可能为( )
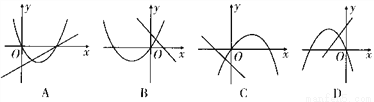
A. A B. B C. C D. D
查看答案抛物线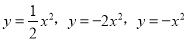 的图象开口最大的是( )
的图象开口最大的是( )
A. 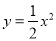 B.
B. 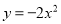 C.
C. 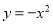 D. 无法确定
D. 无法确定
对于函数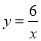 ,下列说法错误的是( )
,下列说法错误的是( )
A. 它的图象在第一、三象限
B. 它的图象既是轴对称图形又是中心对称图形
C. 当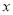 >0时,
>0时, 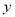 的值随
的值随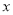 的增大而增大
的增大而增大
D. 当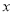 <0时,
<0时, 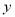 的值随
的值随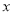 的增大而减小
的增大而减小
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案如图,AC⊥BC于点C,CD⊥AB于点D,其中长度能表示点到直线(或线段)的距离的线段有( )
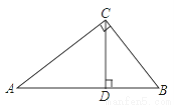
A. 1条 B. 2条 C. 3条 D. 5条
D 【解析】试题解析:表示点C到直线AB的距离的线段为CD, 表示点B到直线AC的距离的线段为BC, 表示点A到直线BC的距离的线段为AC, 表示点A到直线DC的距离的线段为AD, 表示点B到直线DC的距离的线段为BD, 共五条. 故选D.在数轴上,点A表示的数是﹣5,点C表示的数是4,若AB=2BC,则点B在数轴上表示的数是( )
A. 1或13 B. 1 C. 9 D. ﹣2或10
查看答案把方程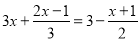 去分母正确的是( )
去分母正确的是( )
A. 18x+2(2x-1)=18-3(x+1) B. 3x+(2x-1)=3-(x+1)
C. 18x+(2x-1)=18-(x+1) D. 3x+2(2x-1)=3-3(x+1)
查看答案一个长为19cm,宽为18cm的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数( )
A. 5个 B. 6个 C. 7个 D. 8个
查看答案下列四种运算中,结果最大的是( )
A. 1+(﹣2) B. 1﹣(﹣2) C. 1×(﹣2) D. 1÷(﹣2)
查看答案(2016四川省南充市)如果向右走5步记为+5,那么向左走3步记为( )
A. +3 B. ﹣3 C. 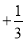 D.
D. 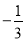
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
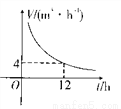
如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。
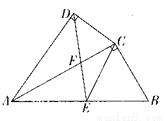
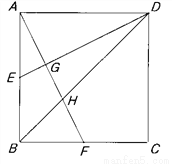
正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
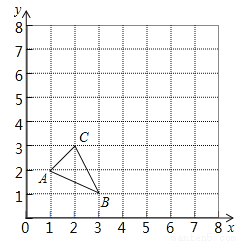
(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
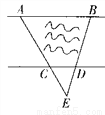
查看答案如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。
若y与x3成反比例,且x=2时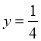 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
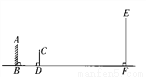
如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。
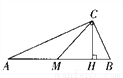
如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.
已知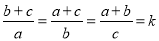 ,则抛物线
,则抛物线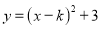 的顶点坐标为____________。
的顶点坐标为____________。
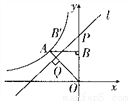
如图,反比例函数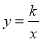 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
A. 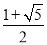 B.
B. 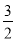 C.
C. 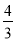 D.
D. 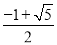
如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2,把△EOF缩小,则点E的对应点E′的坐标为( ).
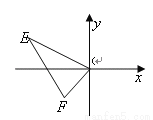
A. (2,-1)或(-2,1) B. (8,-4)或(-8,4) C. (2,-1) D. (8,-4)
查看答案如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A. 2 B. 2.5或3.5 C. 3.5或4.5 D. 2或3.5或4.5
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
对于函数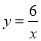 ,下列说法错误的是( )
,下列说法错误的是( )
A. 它的图象在第一、三象限
B. 它的图象既是轴对称图形又是中心对称图形
C. 当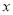 >0时,
>0时, 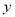 的值随
的值随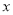 的增大而增大
的增大而增大
D. 当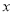 <0时,
<0时, 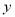 的值随
的值随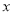 的增大而减小
的增大而减小
二次函数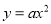 的图象一定过点( )
的图象一定过点( )
A. (0,0) B. (1,2) C. (—1,2) D. 以上都正确
查看答案下列四组线段中,不能组成比例线段的是( )
A. 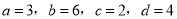
B. 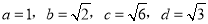
C. 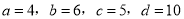
D. 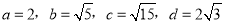
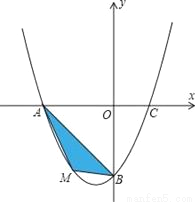
如图,在平面直角坐标系中,已知抛物线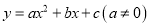 与x轴相交于
与x轴相交于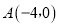 ,C两点
,C两点 与y轴相交于点B
与y轴相交于点B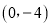 .
.
 a 0,
a 0, 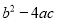
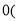 填“
填“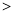 ”或“
”或“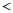 ”
” 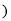 ;
;
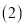 若该抛物线关于直线
若该抛物线关于直线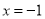 对称,求抛物线的函数表达式;
对称,求抛物线的函数表达式;
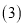 在
在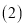 的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为
的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为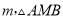 的面积为
的面积为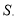 求S关于m的函数关系式,并求出S的最大值;
求S关于m的函数关系式,并求出S的最大值;
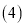 在
在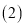 的条件下,若点P是抛物线上的动点,点Q是直线
的条件下,若点P是抛物线上的动点,点Q是直线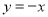 上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
阅读材料:善于思考的小军在解方程组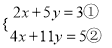 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
【解析】
将方程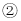 变形:
变形: 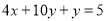 即
即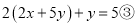
把方程 带入
带入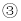 得:
得: 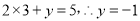
把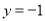 代入
代入 得
得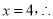 方程组的解为
方程组的解为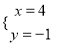 .
.
请你解决以下问题:
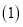 模仿小军的“整体代换”法解方程组
模仿小军的“整体代换”法解方程组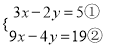
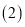 已知
已知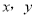 满足方程组
满足方程组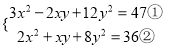 .
.
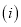 求
求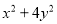 的值;
的值;
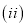 求
求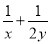 的值.
的值.
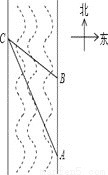
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西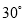 的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西
的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西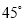 的方向上,请你根据以上数据,求这段河段的宽度
的方向上,请你根据以上数据,求这段河段的宽度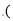 结果保留根号
结果保留根号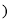
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
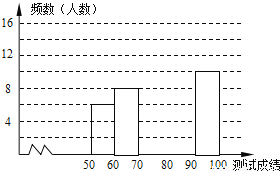
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
 求表中a的值;
求表中a的值;  频数分布直方图补充完整;
频数分布直方图补充完整;
 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
如图,在平面直角坐标系中,一次函数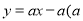 为常数
为常数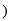 的图象与y轴相交于点A,与函数
的图象与y轴相交于点A,与函数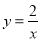 的图象相交于点
的图象相交于点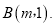
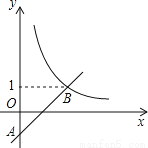
 求点B的坐标及一次函数的解析式;
求点B的坐标及一次函数的解析式;
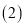 若点P在y轴上,且
若点P在y轴上,且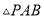 为直角三角形,请直接写出点P的坐标.
为直角三角形,请直接写出点P的坐标.
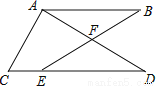
如图, 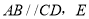 是CD上一点,BE交AD于点
是CD上一点,BE交AD于点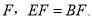 求证:
求证: 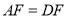 .
.
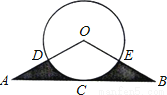
如图, 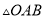 的底边经过
的底边经过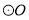 上的点C,且
上的点C,且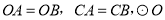 与OA、OB分别交于D、E两点.
与OA、OB分别交于D、E两点.
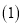 求证:AB是
求证:AB是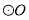 的切线;
的切线;
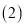 若D为OA的中点,阴影部分的面积为
若D为OA的中点,阴影部分的面积为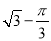 ,求
,求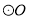 的半径r.
的半径r.
化简: 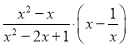
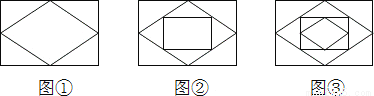
已知:顺次连接矩形各边的中点,得到一个菱形,如图 ;再顺次连接菱形各边的中点,得到一个新的矩形,如图
;再顺次连接菱形各边的中点,得到一个新的矩形,如图 ;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图
;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图 ;如此反复操作下去,则第2014个图形中直角三角形的个数有 个
;如此反复操作下去,则第2014个图形中直角三角形的个数有 个
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图所示的几何体的俯视图是
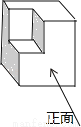
A.  B.
B.  C.
C.  D.
D. 
下列运算正确的是
A. 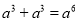 B.
B. 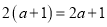 C.
C. 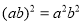 D.
D. 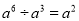
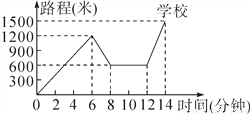
陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?
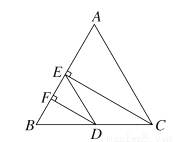
如图,在三角形ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.
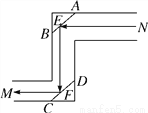
如图,潜望镜中的两个镜片AB和CD是平行的,光线经过镜子反射时,∠AEN=∠BEF,∠EFD=∠CFM,那么进入潜望镜的光线NE和离开潜望镜的光线FM是平行的吗?说明理由.
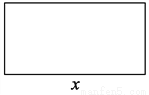
如图所示,用长为20的铁丝焊接成一个长方形,设长方形的一边为x,面积为y,随着x的变化,y的值也随之变化.
(1)写出y与x之间的关系式,并指出在这个变化中,哪个是自变量?哪个是因变量?
(2)用表格表示当x从1变化到9时(每次增加1),y的相应值;
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y |
(3)当x为何值时,y的值最大?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
为让利于民,“百惠大药房”将原价为a元的某药品第1次降价了10%,第2次又降价了5%,则两次降价后的价格可列代数式表示为( )
A. 5%×10%a元 B. (1-10%-5%)a元
C. (1+10%)(1+5%)a元 D. (1-5%)(1-10%)a元
D 【解析】两次降价后的价格可列代数式表示为(1?5%)(1?10%)a元; 故选D比较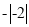 与
与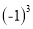 的大小,结果是( )
的大小,结果是( )
A. 前者大 B. 一样大 C. 后者大 D. 无法确定
查看答案多项式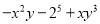 的次数与项数分别是( )
的次数与项数分别是( )
A. 4,3 B. 3,4 C. 5,3 D. 3,3
查看答案下列等式变形正确的是( )
A. 由x+2=3得x=3+2 B. 由-2x=-5得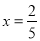
C. 由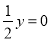 得y=2 D. 由-2=x得x=-2
得y=2 D. 由-2=x得x=-2
2017年上半年某地区用于推进义务教育均衡发展的资金约为210亿,其中“210亿”可用科学计数法表示为( )
A. 0.21×1013 B. 2.1×1012 C. 2.1×1010 D. 2.1×1011
查看答案方程x-1=2x的解是( )
A. x=1 B. x=-1 C. 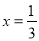 D.
D. 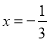
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


 人数
人数