题目内容
8. 将矩形ABCD(如图)绕点C顺时针旋转90°,点A、B、D分别落在点A1、B1、D1处,如果AB=3,BC=4,那么∠AA1D1的正切值是7.
将矩形ABCD(如图)绕点C顺时针旋转90°,点A、B、D分别落在点A1、B1、D1处,如果AB=3,BC=4,那么∠AA1D1的正切值是7.
分析 延长A1 A、D1 B交于点M,由矩形的性质得出∠ABC=∠ADC=90°,CD=AB=3,AD=BC=4,∠ABM=90°,由旋转的性质得出∠A1 D1 C=∠ADC=90°=∠ABM,CD1=CD=3,A1 D1=AD=4,证出AB∥A1 D1,得出△ABM∽△A1 D1 M,由相似三角形的对应边成比例得出$\frac{AB}{{A}_{1}{D}_{1}}=\frac{BM}{{D}_{1}M}$,求出BM=21,得出D1 M=28,再由三角函数的定义即可得出结果.
解答 解:如图所示:延长A1 A、D1 B交于点M,
∵四边形ABCD是矩形,
∴∠ABC=∠ADC=90°,CD=AB=3,AD=BC=4,
∴∠ABM=90°,
由旋转的性质得:∠A1 D1 C=∠ADC=90°=∠ABM,CD1=CD=3,A1 D1=AD=4,
∴AB∥A1 D1,
∴△ABM∽△A1 D1 M,
∴$\frac{AB}{{A}_{1}{D}_{1}}=\frac{BM}{{D}_{1}M}$,
即$\frac{BM}{BM+7}=\frac{3}{4}$,
解得:BM=21,
∴D1 M=21+3+4=28,
∴tan∠AA1D1=$\frac{{D}_{1}M}{{A}_{1}{D}_{1}}$=$\frac{28}{4}$=7;
故答案为:7.
点评 本题考查了矩形的性质、旋转的性质、平行线的判定、相似三角形的判定与性质;熟练掌握旋转的性质和矩形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
19. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若直线y=kx+b平行BD且与正方形ABCD有公共点,则b的取值范围为( )| A. | 1<b<8 | B. | 1≤b≤8 | C. | 2≤b≤8 | D. | 2≤b<8 |
16.某商场为促销某种商品,将定价为5元/件的该商品按如下方式销售:若购买不超过5件商品,按原价销售;若一次性购买超过5件,按原价的八折进行销售.小明现有29元,则最多可购买该商品( )
| A. | 5件 | B. | 6件 | C. | 7件 | D. | 8件 |
20.已知a、b为两个连续整数,且a<$\sqrt{7}$<b,则a+b的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
17.图中的平面展开图是下面名称几何体的展开图,则立体图形与平面展开图不相符的是( )
| A. |  三棱锥 | B. |  长方体 | C. |  正方体 | D. |  圆柱体 |
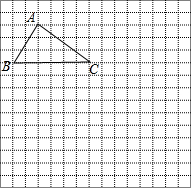 △ABC在网格中的位置如图所示,请根据下列要求解答:
△ABC在网格中的位置如图所示,请根据下列要求解答: 如图,△AOB在平面直角坐标系中,A(1,4),B(3,1),D(5,1);
如图,△AOB在平面直角坐标系中,A(1,4),B(3,1),D(5,1); 如图,写出平面直角坐标系中点A,B,C的坐标,并作出△ABC向右平移3个单位再向下平移2个单位后得到的△A1B1C1
如图,写出平面直角坐标系中点A,B,C的坐标,并作出△ABC向右平移3个单位再向下平移2个单位后得到的△A1B1C1