题目内容
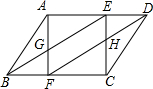 如图,在?ABCD中,点E、F分别是AD、BC上的点,且DE=BF,你能判断四边形GFHE的形状吗?请你说明理由.
如图,在?ABCD中,点E、F分别是AD、BC上的点,且DE=BF,你能判断四边形GFHE的形状吗?请你说明理由.考点:平行四边形的判定与性质
专题:
分析:由?ABCD可得AD∥BCAD=BC,又因为DE=BF,可得四边形BFDE是平行四边形,又由AD=BC,可得AE=CF,从而证得四边形AECF是平行四边形,继而证得四边形GFHE是平行四边形.
解答:解:能,四边形GFHE是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵DE=BF,AD∥BC,
∴四边形BFDE是平行四边形,
∴EG∥FH
∵DE=BF,AD=BC,
∴AE=CF,
又∵AE=CF,AD∥BC,
∴四边形AECF是平行四边形,
∴GF∥EH,
∵EG∥FH,GF∥EH,
∴四边形GFHE是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵DE=BF,AD∥BC,
∴四边形BFDE是平行四边形,
∴EG∥FH
∵DE=BF,AD=BC,
∴AE=CF,
又∵AE=CF,AD∥BC,
∴四边形AECF是平行四边形,
∴GF∥EH,
∵EG∥FH,GF∥EH,
∴四边形GFHE是平行四边形.
点评:本题主要考查平行四边形的性质和判定,熟练掌握平行四边形的性质和判定是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
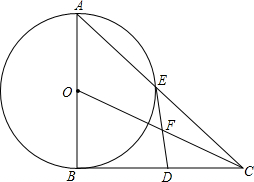 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE.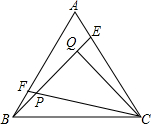 如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=
如图,点E,F分别是正△ABC的边AC,AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE= 已知如图,点B在线段AC上,AB=8cm,AC=18cm,点P,Q分别是AB,AC的中点,求线段PQ的长.
已知如图,点B在线段AC上,AB=8cm,AC=18cm,点P,Q分别是AB,AC的中点,求线段PQ的长.