题目内容
18.先化简,再求值:b2-$\frac{{a}^{3}-a{b}^{2}}{a+b}$÷(a-$\frac{ab-{b}^{2}}{a-b}$),其中a=1,b=$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到结果,把a与b的值代入计算即可.
解答 解:原式=b2-$\frac{a(a+b)(a-b)}{a+b}$•$\frac{a-b}{{a}^{2}-ab-ab+{b}^{2}}$=b2-$\frac{a(a+b)(a-b)}{a+b}$•$\frac{a-b}{(a-b)^{2}}$=b2-a,
当a=1,b=$\sqrt{3}$时,原式=3-1=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
2.若3×27m÷9m=36,则正整数m的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8. 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
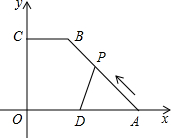 已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,
已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,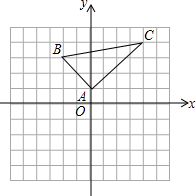 如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).
如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).