题目内容
已知（x3+ax2+x+1）÷（x+1）=x2-bx+1，求a，b的值．
考点：整式的除法
专题：
分析：根据乘除法互为逆运算，所以可以先算（x+1）（x2-bx+1）的积，然后与（x3+ax2+x+1）对应项相等即可求出a，b的值．
解答：解：∵（x3+ax2+x+1）÷（x+1）=x2-bx+1，
∴（x+1）（x2-bx+1）=x3+ax2+x+1，
即：x3-（b-1）x2+（1-b）x+1=x3+ax2+x+1，
∴-（b-1）=a，1-b=1，
解得：a=1，b=0．
∴（x+1）（x2-bx+1）=x3+ax2+x+1，
即：x3-（b-1）x2+（1-b）x+1=x3+ax2+x+1，
∴-（b-1）=a，1-b=1，
解得：a=1，b=0．
点评：此题考查了整式的除法，解题的关键是：根据乘除法互为逆运算，将除法转化为乘法．
练习册系列答案
相关题目
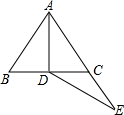如图，已知等边三角形ABC中，AD是BC边上中线，E是AC延长线上一点，且CE=CD，AD=