题目内容
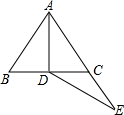 如图,已知等边三角形ABC中,AD是BC边上中线,E是AC延长线上一点,且CE=CD,AD=
如图,已知等边三角形ABC中,AD是BC边上中线,E是AC延长线上一点,且CE=CD,AD=| 6 |
考点:等边三角形的性质
专题:
分析:由条件可求出CD和AD的长,且CD=CE,得出∠CED=∠DAE=30°,得出DE=AD,可求出周长.
解答:解:∵△ABC为等边三角形,AD是BC边上的中线,
∴AD⊥BC,∠DAC=
∠BAC=30°,
∵tan∠DAC=
,
∴
=
,解得CD=3
,则AC=2CD=6
,
∵CD=CE,∠ACD=60°,
∴∠E=
∠ACD=30°=∠DAC,
∴DE=AD=
,
∴AD+DE+AE=2AD+AC+CE=2AD+AC+CD=2
+6
+3
=2
+9
,
即△ADE的周长为2
+9
.
∴AD⊥BC,∠DAC=
| 1 |
| 2 |
∵tan∠DAC=
| CD |
| AD |
∴
| 3 |
| CD | ||
|
| 2 |
| 2 |
∵CD=CE,∠ACD=60°,
∴∠E=
| 1 |
| 2 |
∴DE=AD=
| 6 |
∴AD+DE+AE=2AD+AC+CE=2AD+AC+CD=2
| 6 |
| 2 |
| 2 |
| 6 |
| 2 |
即△ADE的周长为2
| 6 |
| 2 |
点评:本题主要考查等边三角形的性质,由条件证明出DE=AD是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
下面命题:
①若a+b+c=0,则一元二次方程ax2+bx+c=0一定有实数根;
②若一元二次方程ax2+bx+c=0没有实数根,则方程cx2+bx+a=0也一定没有实数根;
③若b=2a+c,则一元二次方程ax2+bx+c=0必有两个不相等的实数根.
其中正确的命题是( )
①若a+b+c=0,则一元二次方程ax2+bx+c=0一定有实数根;
②若一元二次方程ax2+bx+c=0没有实数根,则方程cx2+bx+a=0也一定没有实数根;
③若b=2a+c,则一元二次方程ax2+bx+c=0必有两个不相等的实数根.
其中正确的命题是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
已知五个数2,3,x,5,7的平均数为6,四个2,3,x,y的平均数为7,则y=( )
| A、10 | B、9 | C、8 | D、7 |
 已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于28cm,则DC的长为
已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于28cm,则DC的长为 如图,△ABC中,∠A=60°,∠ACB的平分线CD和∠ABC的平分线BE交于点G.
如图,△ABC中,∠A=60°,∠ACB的平分线CD和∠ABC的平分线BE交于点G.