题目内容
20.先化简,再求值:(6x$\sqrt{\frac{y}{x}}$+$\frac{3}{y}$$\sqrt{x{y}^{3}}$)-(4y$\sqrt{\frac{x}{y}}$+$\sqrt{36xy}$),其中x=$\frac{3}{2}$,y=27.分析 先利用二次根式的性质化简,合并后代入求得数值即可.
解答 解:原式=6$\sqrt{xy}$+3$\sqrt{xy}$-4$\sqrt{xy}$-6$\sqrt{xy}$
=-$\sqrt{xy}$
当x=$\frac{3}{2}$,y=27时,
原式=-$\sqrt{\frac{3}{2}×27}$=-$\frac{9\sqrt{2}}{2}$.
点评 此题考查二次根式的化简求值,注意先化简代数式,再进一步代入求得数值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
9.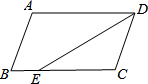 如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
 如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=12cm,AB=8cm,DE平分∠ADC交BC边于点E,则BE等于( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
 如图,画一个三角形,使它与△ABC相似,且相似比为1:2.
如图,画一个三角形,使它与△ABC相似,且相似比为1:2.