题目内容
2.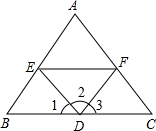 如图,请完成下列各题:
如图,请完成下列各题:(1)如果∠1=∠C,那么DE∥AC(同位角相等,两直线平行);
(2)如果∠1=∠FED,那么EF∥BC(内错角相等,两直线平行);
(3)如果∠FED+∠EFC=180°,那么AC∥ED(同旁内角互补,两直线平行);
(4)如果∠2+∠AED=180°,那么AB∥DF(同旁内角互补,两直线平行).
分析 根据平行线的判定定理对各选项进行逐一分析即可.
解答 解:(1)∵∠1=∠C,∴DE∥AC.
故答案为:∠C,同位角相等,两直线平行;
(2)∵∠1=∠FED,∴EF∥BC.
故答案为:∠FED,内错角相等,两直线平行;
(3)∵∠FED+∠EFC=180°,∴AC∥ED.
故答案为:∠EFC,同旁内角互补,两直线平行;
(4)∵∠2+∠AED=180°,
∴AB∥DF.
故答案为:∠AED,同旁内角互补,两直线平行.
点评 本题考查的是平行线的判定,用到的知识点为:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目
10.下列变形错误的是( )
| A. | 由-4x=3,得x=-$\frac{3}{4}$ | B. | 由2x=2,得x=1 | C. | 由2=-3x,得x=-$\frac{3}{2}$ | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$,得x=$\frac{1}{2}$ |
17. 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )
 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )| A. | ∠C=∠1 | B. | ∠A=∠2 | C. | ∠C=∠3 | D. | ∠A=∠1 |
12.已知x+y=5,xy=3,则x2+y2=( )
| A. | 31 | B. | 28 | C. | 25 | D. | 19 |
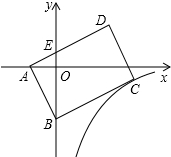 如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.
如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.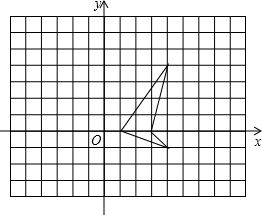 如图,方格纸中有一条可爱美丽的小金鱼
如图,方格纸中有一条可爱美丽的小金鱼