题目内容
7.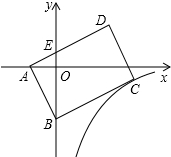 如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.
如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.
分析 首先得出△AEB≌△GBE,再利用四边形BCDE的面积等于△ABE面积的5倍,进而得出AE与BC之间的关系,由△BCF∽△EAO,得出C点坐标,进而求出k的值.
解答 解:如图,作CF⊥y轴于F,作EG⊥BC于G,
∵∠EGB=∠EAB=∠ABG=90°,
∴四边形ABGE是矩形,
在△AEB和△GBE中,
$\left\{\begin{array}{l}{AE=BG}\\{EB=EB}\\{AB=EG}\end{array}\right.$,
∴△AEB≌△GBE(SSS),
∵A、B的坐标分别是A(-1,0)、B(0,-2),
∴AB直线解析式为:y=kx+b,
故将两点代入得出:$\left\{\begin{array}{l}{-k+b=0}\\{b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
故直线AB解析式为:y=-2x-2,
∵AD⊥AB,AO⊥BE,
∴OA2=OE•OB,即12=OE×2,
∴OE=$\frac{1}{2}$,
∴E(0,$\frac{1}{2}$)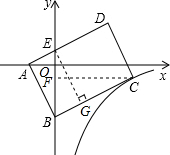
∵S四边形BCDE=5S△AEB
∴S四边形BCDE=5S△GBE
∴S四边形CDEG=4S△GBE
∴CG=2BG=2AE=2$\sqrt{A{O}^{2}+E{O}^{2}}$=$\sqrt{5}$,
∴BG=$\frac{\sqrt{5}}{2}$,
∵∠AEO=∠CBF,∠EOA=∠CFB=90°,
∴△BCF∽△EAO,
∴$\frac{BF}{EO}$=$\frac{CF}{AO}$=$\frac{BC}{AE}$,
∵AE=BG=$\frac{\sqrt{5}}{2}$,BC=BG+CG=$\frac{\sqrt{5}}{2}$+$\sqrt{5}$=$\frac{3\sqrt{5}}{2}$
∴∴$\frac{BF}{EO}$=$\frac{CF}{AO}$=$\frac{BC}{AE}$=3,
∴BF=3EO=$\frac{3}{2}$,CF=3AO=3,
∴OF=OB-BF=2-$\frac{3}{2}$=$\frac{1}{2}$,
设C的坐标为(x,y)则x=3,y=-$\frac{1}{2}$.
故k=xy=3×(-$\frac{1}{2}$)=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查了反比例函数的综合运用,通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标是解题关键.

| A. | (-$\frac{1}{2}$,-$\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{3}$)或(-$\frac{1}{2}$,$\frac{1}{3}$) | D. | (-$\frac{1}{3}$,-$\frac{1}{2}$) |
| 城市 | 北京 | 合肥 | 南京 | 哈尔滨 | 成都 | 南昌 |
| 污染指数 | 354 | 163 | 163 | 45 | 227 | 163 |
| A. | 163和163 | B. | 105和163 | C. | 105和164 | D. | 163和164 |
| A. | a=-1,b=2 | B. | a=-1,b=1 | C. | a=1,b=1 | D. | a=1,b=2 |
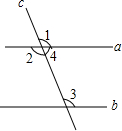 如图所示,已知直线a、b被直线c所截,以下结论:
如图所示,已知直线a、b被直线c所截,以下结论: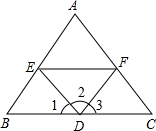 如图,请完成下列各题:
如图,请完成下列各题: