题目内容
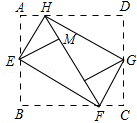 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是( )| A、12厘米 | B、15厘米 |
| C、20厘米 | D、21厘米 |
考点:翻折变换(折叠问题)
专题:
分析:利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.
解答:解:∵∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=
×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,HF=
=
=15,
∴AD=15厘米.
故选:B.
∴∠HEF=∠HEM+∠FEM=
| 1 |
| 2 |
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,HF=
| EH2+EF2 |
| 92+122 |
∴AD=15厘米.
故选:B.
点评:此题主要考查了翻折变换、三角形等知识的掌握情况.错误的主要原因是空间观念以及转化的能力不强,缺乏简单的逻辑推理能力.

练习册系列答案
相关题目
下列图形中,是中心对称的图形是( )
A、 |
B、 |
C、 |
D、 |
| 1 |
| 4 |
| A、4 | ||
| B、-4 | ||
C、-
| ||
D、
|
若x-
=
,则M等于( )
| x2-1 |
| 1 |
| M |
A、x2+
| ||
B、x+
| ||
C、x2-
| ||
D、x-
|
 观察下面一组数:-1,2,-3,4,-5,6,-7,…,将这组数排成如图的形式,按照如图规律排下去,则第10行中从左边数第9个数是( )
观察下面一组数:-1,2,-3,4,-5,6,-7,…,将这组数排成如图的形式,按照如图规律排下去,则第10行中从左边数第9个数是( )| A、-90 | B、90 |
| C、-91 | D、91 |
 如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,则∠ABC=
如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,则∠ABC=