题目内容
已知直线y=x+m与抛物线y=x2相交于两点,则实数m的取值范围 .
考点:二次函数的性质
专题:
分析:联立两函数解析式,消掉y得到关于x的一元二次方程,再根据有两个交点,利用根的判别式列不等式求解即可.
解答:解:联立
消掉y得,x2-x-m=0,
∵直线y=x+m与抛物线y=x2相交于两点,
∴△=b2-4ac=(-1)2-4×1×(-m)=1+4m>0,
解得m>-
.
故答案为:m>-
.
|
∵直线y=x+m与抛物线y=x2相交于两点,
∴△=b2-4ac=(-1)2-4×1×(-m)=1+4m>0,
解得m>-
| 1 |
| 4 |
故答案为:m>-
| 1 |
| 4 |
点评:本题考查了二次函数的性质,联立两函数解析式求交点坐标是常用的方法,本题利用根的判别式列出不等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
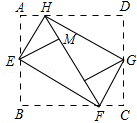 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=9厘米,EF=12厘米,则边AD的长是( )| A、12厘米 | B、15厘米 |
| C、20厘米 | D、21厘米 |
 已知∠β、∠γ与线段c,利用尺规
已知∠β、∠γ与线段c,利用尺规 如图,△ABC内接于⊙O,∠A=40°,则∠BOC=
如图,△ABC内接于⊙O,∠A=40°,则∠BOC= 如图,在矩形ABCD中,AB=2AD=4,以点A为圆心,AB为半径的圆弧交CD于点E,交AD的延长线于点F,则图中阴影部分的面积为
如图,在矩形ABCD中,AB=2AD=4,以点A为圆心,AB为半径的圆弧交CD于点E,交AD的延长线于点F,则图中阴影部分的面积为 如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C14.若P(27,m)在第14段图象C14上,则m=
如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C14.若P(27,m)在第14段图象C14上,则m=