题目内容
16.若抛物线y=ax2+bx+c(a≠0)的顶点坐标为(6,8),则抛物线y=a(3x)2+b(3x)+c(a≠0)的顶点坐标为(2,8);若方程ax2+bx+c=0的两根为-2和8,则a(kx)2+b(kx)+c=0的两根为x=$\frac{8}{k}$或x=-$\frac{2}{k}$(结果用含k的代数式表示).分析 由顶点坐标的公式,整理可用a分别表示出b和c,再代入y=a(3x)2+b(3x)+c(a≠0)可求得其顶点坐标;由ax2+bx+c的两根为-2和8,可用a表示出b和c,再代入a(kx)2+b(kx)+c=0可求得其根.
解答 解:
∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为(6,8),
∴-$\frac{b}{2a}$=6,解得b=-12a,
把点(6,8)代入抛物线解析式可得8=36a+6b+c,
整理可得c=8+36a,
∴y=a(3x)2+b(3x)+c=9ax2-36ax+36a+8=9a(x-2)2+8,
∴该抛物线的顶点坐标为(2,8);
∵方程ax2+bx+c=0的两根为-2和8,
∴-$\frac{b}{a}$=-2+8=6,$\frac{c}{a}$=-2×8,
∴b=-6a,c=-16a,
∴a(kx)2+b(kx)+c=0可化为a(kx)2-6akx-16a=0,
∴k2x2-6kx-16=0,即(kx-8)(kx+2)=0,解得x=$\frac{8}{k}$或x=-$\frac{2}{k}$,
故答案为:(2,8);x=$\frac{8}{k}$或x=-$\frac{2}{k}$.
点评 本题主要考查二次函数的顶点坐标,分别用a表示出b和c是解题的关键.注意整体思想.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
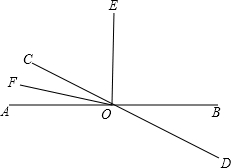 如图所示,已知直线AB、CD相交于点O,OE、OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求∠EOD的度数.
如图所示,已知直线AB、CD相交于点O,OE、OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求∠EOD的度数.