题目内容
4.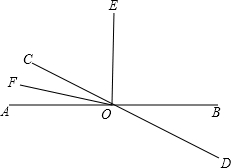 如图所示,已知直线AB、CD相交于点O,OE、OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求∠EOD的度数.
如图所示,已知直线AB、CD相交于点O,OE、OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求∠EOD的度数.
分析 根据对顶角相等得到∠AOC=∠BOD,由角平分线的性质得到∠AOF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠BOD,求得∠AOF=17°,∠BOD=34°,再根据邻补角的性质即可得到结论.
解答 解:∵∠AOC=∠BOD,
∵OF平分∠AOC,
∴∠AOF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠BOD,
∵∠AOF+∠BOD=51°,
∴∠AOF=17°,
∠BOD=34°,
∵∠AOE=90°,
∴∠BOE=180°-∠AOE=90°,
∴∠DOE=90°+34°=124°.
点评 本题考查了角平分线的定义,对顶角相等的性质,角的计算,是基础题,准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
12.如果$\sqrt{x-2}$有意义,那么( )
| A. | x≥0 | B. | x≥2 | C. | x≤2 | D. | 0≤x≤2 |
9.下面调查方式中正确的是( )
| A. | 了解某品牌灯泡的使用寿命用全面调查的方式 | |
| B. | 学校招聘教师,对应聘人员面试用抽样调查的方式 | |
| C. | 旅客上飞机前的安检用全面调查的方式 | |
| D. | 纠正某书稿中的错别字用抽样调查的方式 |
14.计算(-2x)3y的结果是( )
| A. | -6x3y | B. | 6x3y | C. | -8x3y | D. | 8x3y |
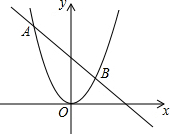 已知函数y1=x2与函数y2=-$\frac{1}{2}$x+3的图象大致如图所示,求抛物线与直线的交点坐标及AB长度.
已知函数y1=x2与函数y2=-$\frac{1}{2}$x+3的图象大致如图所示,求抛物线与直线的交点坐标及AB长度.