题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发运动到点
出发运动到点![]() ,点
,点![]() 以相同的速度从点
以相同的速度从点![]() 出发运动到点
出发运动到点![]() ,两点同时出发,过点
,两点同时出发,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
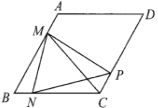
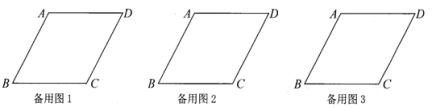
(1)当![]() 和
和![]() 时,请你分别在备用图1,备用图2中画出符合题意的图形;
时,请你分别在备用图1,备用图2中画出符合题意的图形;
(2)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)当点![]() 在线段
在线段![]() 的延长线上时,是否存在某一时刻
的延长线上时,是否存在某一时刻![]() 使
使![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析;(2)当![]() 时,以
时,以![]() 为顶点的四边形是平行四边形 ;(3)
为顶点的四边形是平行四边形 ;(3)![]() 时,
时,![]() .
.
【解析】
(1)根据AM=t![]() 1可得,再根据题意过点过点
1可得,再根据题意过点过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 即可;
即可;
(2) 过![]() 作
作![]() 于
于![]() ,先证明四边形AMPE是平行四边形,从而得到AM=PE,在Rt△ADE中法求得DE=2,再求出PC=2-t,根据要使以
,先证明四边形AMPE是平行四边形,从而得到AM=PE,在Rt△ADE中法求得DE=2,再求出PC=2-t,根据要使以![]() 为顶点的四边形是平行四边形则AM=PC,得到关于t的方程,解方程即可;
为顶点的四边形是平行四边形则AM=PC,得到关于t的方程,解方程即可;
(3) 当![]() 在线段
在线段![]() 延长线上时,可得
延长线上时,可得![]() ,
,![]() ,
,![]() ,再根据
,再根据![]() 得到关于t的方程,解方程即可.
得到关于t的方程,解方程即可.
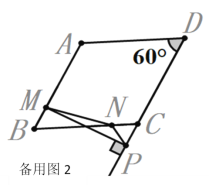
(1)如备用图1、2所示;
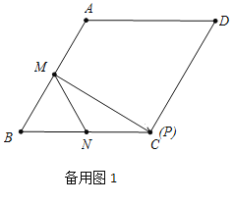
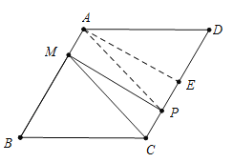
(2)若点![]() 在线段
在线段![]() 上时,过
上时,过![]() 作
作![]() 于
于![]() ,如图
,如图
∵![]()
∴![]()
又在平行四边形![]() 中,
中,![]() ,即
,即![]()
∴四边形![]() 是平行四边形 ,
是平行四边形 ,
∴![]()
由运动可知![]()
∴![]() ,
,
在![]() 中
中
![]()
∴![]() ,
,
![]() ,
,
要使四边形![]() 为平行四边形,则只需
为平行四边形,则只需![]() ,
,
即![]() ,解得,
,解得,![]() ,
,
当![]() 时,以
时,以![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)当![]() 在线段
在线段![]() 延长线上时,假设时,如图
延长线上时,假设时,如图
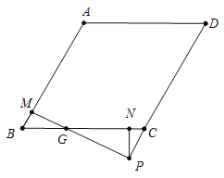
易知![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
故![]() 时,
时,![]() .
.

【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?