题目内容
解方程:x+
=x2-1+
.
| 1+2x |
| 2x2-1 |
考点:无理方程
专题:
分析:将原方程变形整理,运用分类讨论的数学思想,按两种情况分类解析问题即可解决.
解答:解:∵x+
=x2-1+
,
∴
-
=x2-x-1,
若x2-x-1≥0,则
-
≥0,
∴
≥
,整理得:x2-x-1≤0;
综上所述:
,故x2-x-1=0,
解得x=
或
(不合题意,舍去),
经检验x=
是原方程的解.
若x2-x-1≤0,可以用与上述类似的方法、步骤,完成解答,
答案仍是x=
,
故该方程的解为x=
.
| 1+2x |
| 2x2-1 |
∴
| 1+2x |
| 2x2-1 |
若x2-x-1≥0,则
| 1+2x |
| 2x2-1 |
∴
| 1+2x |
| 2x2-1 |
综上所述:
|
解得x=
1+
| ||
| 2 |
1-
| ||
| 2 |
经检验x=
1+
| ||
| 2 |
若x2-x-1≤0,可以用与上述类似的方法、步骤,完成解答,
答案仍是x=
1+
| ||
| 2 |
故该方程的解为x=
1+
| ||
| 2 |
点评:该题主要考查了特殊无理方程的解法问题;解题的关键是将原方程灵活变形,运用分类讨论的数学思想,将无理方程转化为有理方程.

练习册系列答案
相关题目
 如图所示,在圆O中,
如图所示,在圆O中,
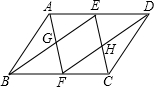 如图,在平行四边形ABCD中,如果E、F分别是边AD、BC的中点,BE交AF于G,DF交EC于H,那么四边形EGFH是平行四边形.请说明:
如图,在平行四边形ABCD中,如果E、F分别是边AD、BC的中点,BE交AF于G,DF交EC于H,那么四边形EGFH是平行四边形.请说明: 如图,已知圆锥的母线AB=12,底面半径2,从B点绕侧面一周回到B点的最短距离是多少?
如图,已知圆锥的母线AB=12,底面半径2,从B点绕侧面一周回到B点的最短距离是多少? 如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标.
如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标. 如图,BC平分∠ABE,DC∠平分ADE.求证:∠E+∠A=2∠C.
如图,BC平分∠ABE,DC∠平分ADE.求证:∠E+∠A=2∠C. 如图,计算∠A+∠B+∠C+∠D+∠E+∠F+∠AGF=
如图,计算∠A+∠B+∠C+∠D+∠E+∠F+∠AGF= 如图,在⊙O中,直径CE⊥弦AB于D,OD=3cm,弦AC=2
如图,在⊙O中,直径CE⊥弦AB于D,OD=3cm,弦AC=2