题目内容
如图所示，在圆O中， |
| AD |
|
| DC |
|
| CB |
考点：圆周角定理,圆心角、弧、弦的关系
专题：
分析：根据等弧对等角及等边对等角可得到∠DAC=∠DCA=∠CDB=∠CBD，再根据三角形外角的性质及三角形内角和定理求解即可．
解答：
解：连接AD，DC，
∵
=
=
，
∴AD=DC=CB，
∴∠DAC=∠DCA=∠CDB=∠CBD，
∵∠DEC=130°
∴∠DCA=∠CDB=25°，∠CEB=50°
∴∠ACB=180°-50°-25°=105°．
解：连接AD，DC，∵
|
| AD |
|
| DC |
|
| CB |
∴AD=DC=CB，
∴∠DAC=∠DCA=∠CDB=∠CBD，
∵∠DEC=130°
∴∠DCA=∠CDB=25°，∠CEB=50°
∴∠ACB=180°-50°-25°=105°．
点评：本题考查了圆周角定理，综合运用圆周角定理和三角形的内角和定理是本题的关键．
练习册系列答案
相关题目
已知二次函数y=ax2+bx的图象如图所示，一元二次方程ax2+bx+c=0有实数根，则c的最大值为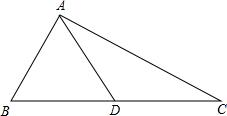
阅读理解题：
已知如图，已知AB⊥AC，∠DAB=∠C，求∠CDA的度数．