题目内容
请画出一次函数y=-
x-3的图象,并且求出该图象与x轴、y轴围成的三角形面积.
| 1 |
| 2 |
考点:一次函数的图象,一次函数图象上点的坐标特征
专题:
分析:先根据直线y=-
x-3求出直线与两坐标轴的交点,再根据三角形的面积公式即可解答.
| 1 |
| 2 |
解答:解:如图所示,直线AB就是一次函数y=-
x-3的图象;

∵函数的解析式可知,函数图象与x轴的交点坐标为(-6,0),与y轴的交点坐标为(0,-3),
∴直线y=-
x-3与两坐标轴围成的三角形面积=
×6×3=9.
| 1 |
| 2 |

∵函数的解析式可知,函数图象与x轴的交点坐标为(-6,0),与y轴的交点坐标为(0,-3),
∴直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题属简单题目,解答此题的关键是熟知两坐标轴上点的坐标特点,及三角形的面积公式.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
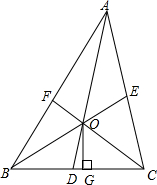 如图,△ABC中,O是内角平分线AD、BE、CF的交点.
如图,△ABC中,O是内角平分线AD、BE、CF的交点.