题目内容
14. 如图,AB⊥BC于B,DC⊥BC于C,AC,BD交于E点,EO⊥BC于O,AB=20,CD=80,则OE=16.
如图,AB⊥BC于B,DC⊥BC于C,AC,BD交于E点,EO⊥BC于O,AB=20,CD=80,则OE=16.
分析 由已知条件得到AB∥OE∥DC,推出△CEO∽△CAB,△BEO∽△BDC,根据相似三角形的性质证得$\frac{OE}{AB}=\frac{CE}{BC}$①,$\frac{OE}{CD}=\frac{BE}{BC}$②,①+②得,$\frac{OE}{AB}+\frac{OE}{CD}=\frac{CE}{BC}+\frac{BE}{BC}$=1,代入数据即可得到结论.
解答 解:∵AB⊥BC于B,DC⊥BC于C,EO⊥BC于O,
∴AB∥OE∥DC,
∴△CEO∽△CAB,
∴$\frac{OE}{AB}=\frac{CE}{BC}$①,
∴△BEO∽△BDC,
∴$\frac{OE}{CD}=\frac{BE}{BC}$②,
①+②得,$\frac{OE}{AB}+\frac{OE}{CD}=\frac{CE}{BC}+\frac{BE}{BC}$=1,
∴$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OE}$,
∵AB=20,CD=80,
∴OE=16.
故答案为:16.
点评 本题考查了相似三角形的判定和性质,平行线的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
6.若x满足x2=$\frac{9}{4}$,则x的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | ±$\frac{2}{3}$ |
2.芳芳在平面直角坐标系画了一个二次函数的图象,并将该图象的特点写在如图所示的卡片上,则该二次函数的解析式为( )
①开口向下;②顶点是原点;③过点(6,-6).
①开口向下;②顶点是原点;③过点(6,-6).
| A. | y=-$\frac{1}{6}{x}^{2}$ | B. | y=$\frac{1}{6}{x}^{2}$ | C. | y=-6x2 | D. | y=6x2 |
19.若两个有理数之和大于0,则这两个数一定不是( )
| A. | 两个负数 | B. | 两个正数 | ||
| C. | 一个正数,一个负数 | D. | 一个正数,一个零 |
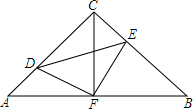 如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.
如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16. 如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.
如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.