题目内容
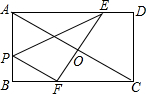 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,且线段EF过矩形对角线AC的中点,PF∥AC,则EF:BF的最小值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:矩形的性质
专题:
分析:过点O作OH⊥BC于H,设AB=x,BF=y,然后表示出FH、OH,再利用勾股定理列式求出OF,然后表示出EF,再求出比值,然后利用根的判别式解答即可.
解答: 解:如图,过点O作OH⊥BC于H,设AB=x,BF=y,
解:如图,过点O作OH⊥BC于H,设AB=x,BF=y,
∵AD=2AB,
∴AD=2x,
∵线段EF过矩形对角线AC的中点,
∴FH=x-y,OH=
x,
由勾股定理得,OF=
,
由矩形的对称性,EF=2
,
设EF:BF=m,
则m2=
,
整理得,(m2-4)y2+8xy-5x2=0,
△=(8x)2-4(m2-4)×(-5x2)≥0,
解得m2≥
,
所以,m≥
,
所以,m的最小值是
,
即EF:BF的最小值是
.
故选A.
 解:如图,过点O作OH⊥BC于H,设AB=x,BF=y,
解:如图,过点O作OH⊥BC于H,设AB=x,BF=y,∵AD=2AB,
∴AD=2x,
∵线段EF过矩形对角线AC的中点,
∴FH=x-y,OH=
| 1 |
| 2 |
由勾股定理得,OF=
(x-y)2+(
|
由矩形的对称性,EF=2
(x-y)2+(
|
设EF:BF=m,
则m2=
| 4(x-y)2+x2 |
| y2 |
整理得,(m2-4)y2+8xy-5x2=0,
△=(8x)2-4(m2-4)×(-5x2)≥0,
解得m2≥
| 4 |
| 5 |
所以,m≥
2
| ||
| 5 |
所以,m的最小值是
2
| ||
| 5 |
即EF:BF的最小值是
2
| ||
| 5 |
故选A.
点评:本题考查了矩形的性质,主要利用了矩形的性质,勾股定理,根的判别式,作辅助线构造出直角三角形并利用根的判别式列出不等式是解题的关键.

练习册系列答案
相关题目
下列变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上的两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是
如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上的两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是 如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.
如图,在△ABC中,∠ABC=45°,H是高AD和BE的交点,G、F分别是BH和AC的中点,试探究DG与DF之间的关系,并证明你的结论.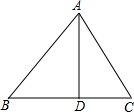 如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是
如图,在△ABC中,AD⊥BC,垂足为D.若AD=4,BC=7,∠B=45°,则AC边的长是 如图,在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,0),AB的垂直平分线交x轴于点C,交AB于点D,求△AOC的周长.
如图,在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,0),AB的垂直平分线交x轴于点C,交AB于点D,求△AOC的周长.