题目内容
15. 如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.
如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.(1)求证:∠C=2∠ADE;
(2)若$\frac{OE}{OA}$=$\frac{3}{5}$,且BC=6,求⊙O的半径.
分析 (1)如图所示:连接OD、OC,先证明Rt△COD≌Rt△COB,∠DOC=∠BOC,然后由OD=OE,得到∠DEO=∠EDO,结合三角形外角的性质可知∠DE0=∠COB,从而得到DE∥OC,由平行线的性质可知∠DCO=∠ADE,故此∠C=2∠ADE;
(2)先证明△AOD∽△ACB,由相似三角形的性质可知$\frac{OA}{OD}=\frac{AC}{BC}$,从而可求得AC=10,AD=4,在Rt△AOD中,由勾股定理得列方程求解即可.
解答 解:(1)如图所示:连接OD、OC.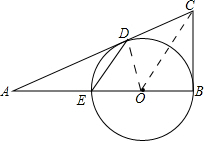
∵线段CD、CB分别与⊙O相切于D、B两点,
∴OD⊥AC,OB⊥BC.
在Rt△COD和Rt△COB中,
$\left\{\begin{array}{l}{OC=OC}\\{OD=OB}\end{array}\right.$,
∴Rt△COD≌Rt△COB.
∴∠DOC=∠BOC.
∵OD=OE,
∴∠DEO=∠EDO.
∵∠DEO+∠EDO=∠DOC=∠BOC.
∴∠DE0=∠COB.
∴DE∥OC.
∴∠DCO=∠ADE.
∴∠C=2∠ADE.
(2)设OE=OD=3x,则OA=5x.
∵∠A=∠A,∠ODA=∠CBA,
∴△AOD∽△ACB.
∴$\frac{OA}{OD}=\frac{AC}{BC}$,即$\frac{3x}{5x}=\frac{6}{AC}$,
解得:AC=10.
∵DC=BC=6,
∴AD=4.
在Rt△AOD中,由勾股定理得:AO2=AD2+OD2,即:(5x)2=(3x)2+42,
解得:x=1或x=-1(舍去).
∴OE=3.
∴⊙O的半径为3.
点评 本题主要考查的是切线的性质、相似三角形的性质和判定、勾股定理,由相似三角形的性质求得AC=10,AD=4是解题的关键.

练习册系列答案
相关题目
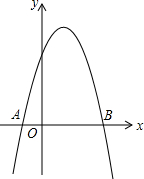 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0).
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0).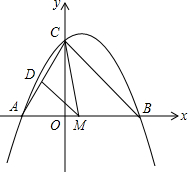 如图,二次函数y=-$\frac{1}{2}$x2+x+4与x轴交于A、B两点,与y轴交于点C.
如图,二次函数y=-$\frac{1}{2}$x2+x+4与x轴交于A、B两点,与y轴交于点C.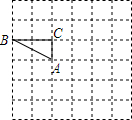 如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.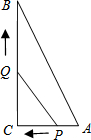 如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问:
如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问: