题目内容
4.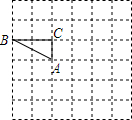 如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.(1)画出旋转后的△AB′C′;
(2)以点C为坐标原点,线段BC、AC所在直线分别为x轴,y轴建立直角坐标系,请直接写出点B′的坐标(1,1);
(3)写出△ABC在旋转过程中覆盖的面积$\frac{5}{4}$π+1.
分析 (1)利用网格特点和旋转的性质画出点B和C的对应点B′、C′,即可得到△AB′C′;
(2)建立直角坐标系,然后写出点B′的坐标;
(3)根据扇形面积公式,计算S扇形BAB′+S△B′AC′,即可得到△ABC在旋转过程中覆盖的面积.
解答 解:(1)如图,△AB′C′为所作;
(2)如图,点B′的坐标为(1,1);
(3)△ABC在旋转过程中覆盖的面积=S扇形BAB′+S△B′AC′=$\frac{90•π•(\sqrt{5})^{2}}{360}$+$\frac{1}{2}$×1×2=$\frac{5}{4}$π+1.
故答案为(1,1),$\frac{5}{4}$π+1.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
12. 如图,图中x的值是( )
如图,图中x的值是( )
 如图,图中x的值是( )
如图,图中x的值是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
19.若分式$\frac{x-3}{x+4}$有意义,则x的取值应满足( )
| A. | x≠3 | B. | x≠4 | C. | x≠-4 | D. | x≠-3 |
9.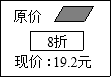 如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
 如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )| A. | 15.36元 | B. | 16元 | C. | 24元 | D. | 23.04元 |
16.单项式-$\frac{3}{5}$a2b2c的次数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.
如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.