题目内容
11.基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2-x-2=0可通过因式分解化为(x-2)(x+1)=0,由基本事实得x-2=0或x+1=0,即方程的解为x=2或x=-1.(1)试利用上述基本事实,解方程:2x2-x=0:
(2)解方程:(x+1)(x+2)+$\frac{1}{4}$=0.
分析 (1)左边因式分解可得:x(2x-1)=0,从而得出x=0或2x-1=0,解之可得;
(2)整理成一般式后因式分解法求解可得.
解答 解:(1)方程左边因式分解可得:x(2x-1)=0,
∴x=0或2x-1=0,
解得:x=0或x=$\frac{1}{2}$;
(2)原方程整理可得:x2+3x+$\frac{9}{4}$=0,
左边因式分解可得:(x+$\frac{3}{2}$)2=0,
∴x+$\frac{3}{2}$=0,
解得:x=-$\frac{3}{2}$.
点评 本题主要考查因式分解法解一元二次方程,熟练掌握因式分解的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

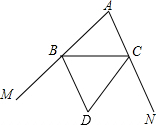 已知:如图,BD,CD分别是△ABC的外角∠MBC、∠NCB的平分线,且交于点D.求证:点D在∠A的平分线上.
已知:如图,BD,CD分别是△ABC的外角∠MBC、∠NCB的平分线,且交于点D.求证:点D在∠A的平分线上. 如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.
如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.