Question

12．已知，ABC中，AC=BC，∠ACB=90°，D为AB的中点，若E在直线AC上任意一点，DF⊥DE，交直线BC于F点，G为EF的中点，延长CG与AB交于点H．
（1）若E在边AC上．①试说明DE=DF；②试说明CG=GH；
（2）若AE=6，CH=10，求边AC的长．

Answer 1

分析 （1）①连接CD，由直角三角形斜边上的中线性质得出CD=AD=BD，CD⊥AB，证出∠EDA=∠CDF，由ASA证明△ADE≌△CDF，即可得出结论；
②连接CD、DG，由直角三角形斜边上的中线性质得出CG=EG=FG，DG=EG=FG，得出CG=DG，因此∠GCD=∠GDC，由角的互余关系得出∠GHD=∠HDG，证出GH=GD，即可得出结论；
（2）分两种情况：①当E在线段AC上时，CG=GH=EG=GF，得出CH=EF=10，由（1）得出AE=CF=6，由勾股定理得出CE，即可得出结论；
②当E在线段CA延长线上时，AC=EC-AE=8-6=2；即可得出结果．

解答 （1）①证明：连接CD，如图1所示：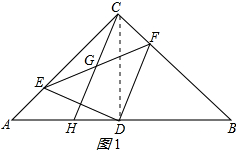
∵∠ACB=90°，AC=BC，D为AB的中点，
∴CD=AD=BD，CD⊥AB，∠EDA+∠EDC=90°，∠DCF=∠DAE=45°，
∵DF⊥DE，
∴∠EDF=∠EDC+∠CDF=90°，
∴∠EDA=∠CDF，
在△ADE和△CDF中，$\left\{\begin{array}{l}{∠DCF=∠DAE}\\{CD=AD}\\{∠CDF=∠ADE}\end{array}\right.$，
∴△ADE≌△CDF（ASA），
∴DE=DF；
②证明：连接DG，如图2所示：
∵∠ACB=90°，G为EF的中点，
∴CG=EG=FG，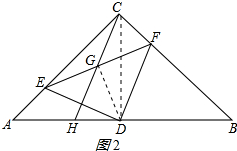
∵∠EDF=90°，G为EF的中点，
∴DG=EG=FG，
∴CG=DG，
∴∠GCD=∠GDC，
∵CD⊥AB，
∴∠CDH=90°，
∴∠GHD+∠GCD=90°，∠HDG+∠GDC=90°，
∴∠GHD=∠HDG，
∴GH=GD，
∴CG=GH；
（2）解：分两种情况：
①当E在线段AC上时，CG=GH=EG=GF，
∴CH=EF=10，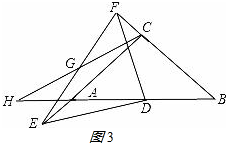
由（1）①知：△ADE≌△CDF，
∴AE=CF=6，
在Rt△ECF中，由勾股定理得：
CE=$\sqrt{E{F}^{2}-C{F}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∴AC=AE+EC=6+8=14；
②当E在线段CA延长线上时，如图3所示：
AC=EC-AE=8-6=2，
综上所述，AC=14或2．

点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、直角三角形斜边上的中线性质、勾股定理、等腰三角形的判定等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．