题目内容
17. 如图,AD为△ABC的中线,BE为三角形ABD中线.
如图,AD为△ABC的中线,BE为三角形ABD中线.(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
分析 (1)根据过直线外一点作已知直线的垂线的方法作图即可;
(2)利用三角形中线的性质得出S△BDE=$\frac{1}{4}$S△ABC,进而借助三角形面积公式求出即可.
解答 解;(1)如图所示:
(2)∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△ABD=$\frac{1}{2}$S△ABC,S△BDE=$\frac{1}{2}$S△ABD,
∴S△BDE=$\frac{1}{4}$S△ABC,
∵△ABC的面积为40,BD=5,
∴$\frac{1}{2}$×5×EF=10,
∴EF=4.
点评 此题主要考查了基本作图以及三角形中线的性质,根据三角形中线平分三角形面积得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | “彩票中奖的概率为1%”,表示买100张彩票一定会中奖 |
4.下列判断中,正确的是( )
| A. | 一个有理数的相反数一定是负数 | B. | 一个非正数的绝对值一定是正数 | ||
| C. | 任何有理数的绝对值都是正数 | D. | 任何有理数的绝对值都不是负数 |
 如图,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.求证:AF=BE.
如图,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.求证:AF=BE. 已知,ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点,G为EF的中点,延长CG与AB交于点H.
已知,ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点,G为EF的中点,延长CG与AB交于点H.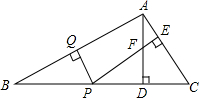 如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC. 如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是方程x2-2$\sqrt{3}$x+$\frac{1}{4}$(m2-2m+13)=0的两个实数根.
如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是方程x2-2$\sqrt{3}$x+$\frac{1}{4}$(m2-2m+13)=0的两个实数根. 如图,等腰直角△ABC与等腰直角△CDE,连接AD、BE,M为AD中点,连接MC并延长交BE于N.
如图,等腰直角△ABC与等腰直角△CDE,连接AD、BE,M为AD中点,连接MC并延长交BE于N.