题目内容
17. 如图所示,△ABC中,∠ABC=90°,AD为∠BAC的平分线,∠C=30°,BE⊥AD于E点,求证:AC-AB=2BE.
如图所示,△ABC中,∠ABC=90°,AD为∠BAC的平分线,∠C=30°,BE⊥AD于E点,求证:AC-AB=2BE.
分析 根据直角三角形30°的角所对的直角边是斜边的一半即可证得结论.
解答 解:∵△ABC中,∠ABC=90°,∠C=30°,
∴∠BAC=60°,AC=2AB,
∵AD为∠BAC的平分线,
∴$∠BAE=\frac{1}{2}∠BAC=30°$,
∵BE⊥AD,
∴∠AEB=90°.
∴AB=2BE,
∴AC-AB=2AB-AB=AB=2BE.
即AC-AB=2BE.
点评 本题考查了据直角三角形30°的角所对的直角边是斜边的一半的性质的应用,熟练掌握和灵活应用该性质是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.下列叙述正确的是( )
| A. | 一个数的相反数一定是负数 | B. | 一个数的绝对值一定是正数 | ||
| C. | 一个数的绝对值一定不是负数 | D. | 一个数的绝对值一定是负数 |
5.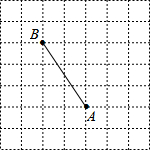 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 12个 |
6.观察下列球的排列规律(其中●是实心球,○是空心球):
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…
从第1个球起到第2012个球止,共有实心球的个数为( )
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…
从第1个球起到第2012个球止,共有实心球的个数为( )
| A. | 598 | B. | 602 | C. | 604 | D. | 608 |
7.一次函数y=5x-2013的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知:如图,在△ABC中,DE∥BC,DF∥AC,求证:$\frac{AC}{CE}=\frac{BC}{BF}$.
已知:如图,在△ABC中,DE∥BC,DF∥AC,求证:$\frac{AC}{CE}=\frac{BC}{BF}$. 如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$).
如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$). 在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.
在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.