题目内容
20.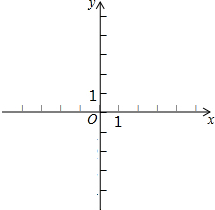 平面上有四个点它们的坐标分别是,A(2,-4),B(4,-4),C(4,-1),D(2,-1)
平面上有四个点它们的坐标分别是,A(2,-4),B(4,-4),C(4,-1),D(2,-1)(1)顺次连接A、B、C、D围成的四边形是什么图形?
(2)这个四边形的面积是多少?
(3)将这个四边形向上平移3个单位长度,四边形的四个顶点的坐标变为多少?此时新的图形面积是多少?若点A向左移动两个单位,其余点不动,此时面积又是多少?画出平移后的图形.
分析 (1)根据题意结合各点坐标在坐标系中标出即可;
(2)利用矩形面积求法得出即可;
(3)利用平移的性质得出平移后图形以及其面积,再利用一般四边形面积求法得出即可.
解答  解:(1)如图所示,四边形ABCD是矩形(长方形);
解:(1)如图所示,四边形ABCD是矩形(长方形);
(2)四边形ABCD的面积=AB×DC=2×3=6;
(3)如图所示:四边形A1B1C11即为所求,
各顶点坐标A1(2,-1),B1(4,-1),C1(4,2),D1(2,2),
新图形面积为6,
点A向左移动2个单位后坐标为(0,-4),
此时新图形面积为:6+$\frac{2×3}{2}$=9.
点评 此题主要考查了平移变换以及四边形面积求法,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
12.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式.
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式.
9.下列各数中,介于2和3之间的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{4}$ | D. | $\sqrt{5}$ |
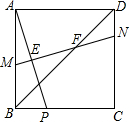 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长是( )
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长是( )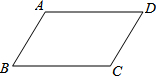 如图,在平行四边形ABCD中,∠A+∠C=240°,则∠B=60度.
如图,在平行四边形ABCD中,∠A+∠C=240°,则∠B=60度.