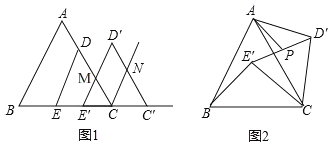Question

【题目】如图，△ABC中，点E、P在边AB上，且AE=BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为，四边形EFQP的面积为，四边形PQCB的面积为

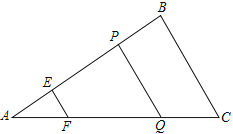
（1）求证：EF＋PQ=BC

（2）若＋=，求的值

（3）若－=，直接写出的值

Answer 1

【答案】见解析；2；．

【解析】

试题过点Q作QD∥PB，从而得到四边形PQDB为平行四边形，根据平行四边形性质得到PQ=BD，PB=QD，∠B=∠QDC，然后再证明△AEF和△QDC全等，从而得出答案；过点A作AH⊥BC于H，分别交EF、PQ于M、N，设EF=a，PQ=b，AM=h，则BC=a+b，根据三角形相似得出，从而求出AN和MN的长度，然后分别求出、和的代数式，然后根据三者之间的关系求出a和b的关系，然后得出答案；根据（2）的同样方法得出答案．

试题解析：（1）如图所示，过点Q作QD∥PB

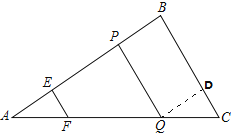
∵PQ∥BC，QD∥BP ∴四边形PQDB为平行四边形 ∴PQ=BD，PB=QD ∠B=∠QDC

∵AE=BP ∴AE=QD ∵EF∥BC ∴∠AFE=∠C ∠AEF=∠B ∴∠AEF=∠QDC

∴△AEF≌△QDC ∴EF=CD ∴BC=BD+CD=PQ+EF

（2）如图，过点A作AH⊥BC于H，分别交EF、PQ于M、N，

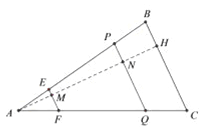
设EF=a，PQ=b，AM=h，则BC=a+b ∵∴AN=h MN=（－1）h

则：=ah=（a+b）（－1）h=（b+a+b）h

∵+=∴ah+（b+a+b）h=（a+b）（－1）h ∴b=3a ∴=2

（3）