Question

【题目】如图，抛物线与x轴相交于A（3，0）、B两点，与y轴交于点C（0，3），点B在x轴的负半轴上，且.

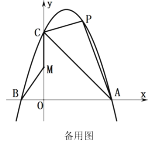
（1）求抛物线的函数关系式；

（2）若P是抛物线上且位于直线上方的一动点，求的面积的最大值及此时点P的坐标；

（3）在线段上是否存在一点M，使的值最小？若存在，请求出这个最小值及对应的M点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）的面积的最大值为，此时；（3）当时，的最小值为.

【解析】

（1）根据求出B点坐标，设交点式，用待定系数法即可求出函数关系式；

（2）作PD⊥x轴，与线段AC相交于D，根据表示的面积，利用二次函数的性质即可求出的面积的最大值及此事P点坐标；

（3）构造CM为斜边的等腰三角形，它的直角顶点为第一象限内的N，可得出=最小值即为BN.设可表示N点坐标，继而可表示，利用二次函数的性质即可求的最小值，以及此时M点坐标.

解：（1）∵，

∴OA=3，OB=1

∴

∴设抛物线的交点式为，

将代入得，解得

∴，

即该抛物线的函数关系式为.

（2）作PD⊥x轴，与线段AC相交于D.

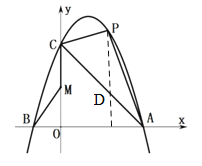
设直线AC：y=kx+d

将,分别代入

得，解得，

所以y=-x+3.

设，则，

设△DCP以PD为底时高为h1，△DAP以PD为底时高为h2，则因为，所以时取得最大值为..

故的面积的最大值为，此时.

（3）存在，如下图，作以CM为斜边的等腰三角形，它的直角顶点为第一象限内的N点，

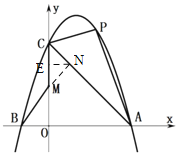
∵△MCN为等腰直角三角形，

∴MN=,即要使最短，只需要最短为BN即可，

设则，

∴

当时，取得最小值为8，即.

当时，的最小值为.