Question

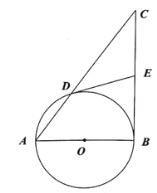
【题目】如图，在等边△ABC内有一点D，AD=5，BD=6，CD=4，将△ABD绕点A逆时针旋转，使AB与AC重合，点D旋转到点E，则∠CDE的正切值为 ．

Answer 1

【答案】.

【解析】

试题解析：∵△ABC为等边三角形，

∴AB=AC，∠BAC=60°，

∵△ABD绕A点逆时针旋转得△ACE，

∴AD=AE=5，∠DAE=∠BNAC=60°，CE=BD=6，

∴△ADE为等边三角形，

∴DE=AD=5，

过E点作EH⊥CD于H，如图，

设DH=x，则CH=4-x，

在Rt△DHE中，EH2=52-x2，

在Rt△DHE中，EH2=62-（4-x）2，

∴52-x2=62-（4-x）2，解得x=，

∴EH=，

在Rt△EDH中，tan∠HDE=，

即∠CDE的正切值为．