题目内容
19．已知a、b、c是△ABC的三边，化简：|-a+b-c|+|a-b-c|+|b+c-a|=-a+b+3c．分析 根据三角形的三边关系“两边之和＞第三边，两边之差＜第三边”，判断式子的符号，再根据绝对值的意义去掉绝对值即可．
解答 解：根据三角形的三边关系，两边之和大于第三边，
得a-b-c＜0，b-c-a＜0，c+b-a＞0．
∴|-a+b-c|+|a-b-c|+|b+c-a|=a-b+c-a+c+b+c+b-a
=-a+b+3c，
故答案为：-a+b+3c．
点评 本题考查了三角形的三边关系、绝对值及整式的加减，注意三角形的三边关系和绝对值的性质的综合运用．
练习册系列答案
名校课堂系列答案
相关题目
9．反比例函数y=$\frac{k}{x}$的自变量x满足2≤x≤4，函数值y满足$\frac{1}{2}$≤y≤1，则这个反比例函数为（ ）
| A． | y=$\frac{1}{x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{4}{x}$ | D． | y=$\frac{1}{2x}$ |
10．在△ABC中，∠BAC=90°，AB=3，AC=4，D是BC的中点，则BD的长为（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | 2 | D． | $\frac{3}{2}$ |
如图，在△ABC中，AB=AC，∠1=∠2，求证：∠3=∠4．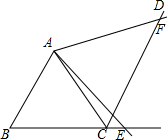
已知，如图，△ABC为等边三角形，CD∥AB，点E、F分别在BC延长线及CD上，∠EAF=60°，求证：BE=CF．
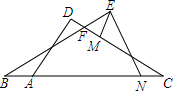已知，如图，∠EBN+∠FCA=∠MEN，AB=CN，EN=AD．EM∥AD．探究BF与CF之间的数量关系．