题目内容
15.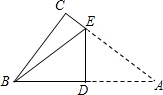 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$.
如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$.
分析 由翻折的性质可知ED⊥AB,∠DEA=∠BEA,然后可证明∠BED=∠ABC,最后根据锐角三角函数的定义求解即可.
解答 解:由翻折的性质可知:ED⊥AB,∠DEA=∠BEA.
∵∠A+∠DEA=90°,∠CBA+∠A=90°,
∴∠DEA=∠CBA.
∴∠BED=∠CBA.
∴tan∠BED=tan∠CBA=$\frac{AC}{BC}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查的是翻折的性质、锐角三角函数的定义,证得∠BED=∠CBA是解题的关键.

练习册系列答案
相关题目
5. 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
20.为了提高土地利用率,将小麦、玉米、黄豆三种农作物套种在一起,俗称“三种三收”,现将面积为10亩的一块农田进行“三种三收”套种,为保证主要农作物的种植比例.要求小麦的种植面积占总面积的60%,下表是三种农作物的亩产量及销售单价的对应表:
(1)设玉米的种值面积为x亩,三种农作物的总售价为y元,写出y与x的函数关系式;
(2)在保证小麦种植面积的情况下,玉米、黄豆同时均按整亩数套种,有几种“三种三收”套种方案?
(3)在(2)中的种植方案中,采用哪种套种方案才能使总销售价最高?最高价是多少?
| 小麦 | 玉米 | 黄豆 | |
| 亩产量(千克) | 600 | 900 | 330 |
| 销售单价(元/千克) | 2 | 1 | 2.5 |
(2)在保证小麦种植面积的情况下,玉米、黄豆同时均按整亩数套种,有几种“三种三收”套种方案?
(3)在(2)中的种植方案中,采用哪种套种方案才能使总销售价最高?最高价是多少?
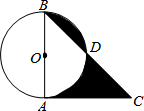 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,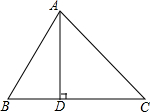 如图,在△ABC中,AD⊥BC于D,tan∠BAD=$\frac{1}{2}$,∠ACD=45°,AB=5,求AC的长.
如图,在△ABC中,AD⊥BC于D,tan∠BAD=$\frac{1}{2}$,∠ACD=45°,AB=5,求AC的长.
 如图,圆柱的底面半径为3πcm,高为4πcm,小毛虫在圆柱表面爬行,从点A爬到点B的最短路程是多少?(结果保留π)
如图,圆柱的底面半径为3πcm,高为4πcm,小毛虫在圆柱表面爬行,从点A爬到点B的最短路程是多少?(结果保留π)