题目内容
5. 如图,圆柱的底面半径为3πcm,高为4πcm,小毛虫在圆柱表面爬行,从点A爬到点B的最短路程是多少?(结果保留π)
如图,圆柱的底面半径为3πcm,高为4πcm,小毛虫在圆柱表面爬行,从点A爬到点B的最短路程是多少?(结果保留π)
分析 根据圆柱展开是个长方形,根据两点之间线段最短,可求出解.
解答 解 解:如图所示:
解:如图所示:
∵AD=2π•3π÷2=3π2(cm),BD=4πcm.
∴在Rt△ABD中,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=π$\sqrt{9{π}^{2}+16}$(cm).
从A点爬到点B的最短路程是:π$\sqrt{9{π}^{2}+16}$(cm).
点评 本题考查平面展开最短路径问题,关键知道圆柱展开图是长方形,根据两点之间线段最短可求出解.

练习册系列答案
相关题目
10.某商品连续两次降价,每次都降20%后的价格为36元,则原价是( )
| A. | 56.25元 | B. | 51.84元 | C. | 25元 | D. | 23.04元 |
17.若方程x2+ax+b=0中有一个根为0,另一个根非0,则a、b的值是( )
| A. | a=0,b=0 | B. | a≠0,b=0 | C. | a=0,b≠0 |
14.有一个数值转换器,原理如下:

当输入的x=9时,输出的y等于( )

当输入的x=9时,输出的y等于( )
| A. | 2 | B. | 8 | C. | $\sqrt{3}$ | D. | $±\sqrt{3}$ |
15.在比例尺为1:400000的工程示意图上,图上距离约为5.3cm,它的实际长度约为( )
| A. | 0.212km | B. | 2.12km | C. | 21.2km | D. | 212km |
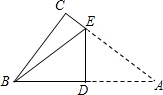 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$.
如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是$\frac{3}{2}$. 在所给的数轴上用字母“A、B、C”分别表示出以下各数:2.5,3$\frac{1}{4}$,-3,并回答问题:这3个数中表示最大数与最小数的两点之间相距多少个单位?
在所给的数轴上用字母“A、B、C”分别表示出以下各数:2.5,3$\frac{1}{4}$,-3,并回答问题:这3个数中表示最大数与最小数的两点之间相距多少个单位?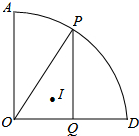 如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.
如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.