题目内容
9.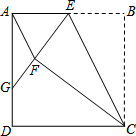 如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
分析 (1)由翻折的性质可知,∠BEC=∠FEC,EB=EF,由∵AF∥CE可证得∠EAF=∠EFA,从而得到EA=EF,故此可知EA=EB,即点E为AB的中点;
(2)如图所示,连接CG,由DC=FC,∠GFC=∠D,FC=DC,从而可得到Rt△GFC≌Rt△GDC,故此GF=GD;
(3)AG=10-x,AE=10-y,GE=x+y,在Rt△AEG中由勾股定理可知:AG2+AE2=GE2,从而可得到y=$\frac{100-10x}{10+x}$.
解答 解:(1)由翻折的性质可知,∠BEC=∠FEC,EB=EF
∵AF∥CE,
∴∠BEC=∠EAF,∠FEC=∠EFA.
∴∠EAF=∠EFA.
∴EA=EF.
∴EA=EB,即点E为AB的中点.
(2)如图所示,连接CG.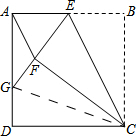
在正方形ABCD中,∠D=∠B=90°,DC=BC,
由翻折的性质可知:∠EFC=∠B=90°,BC=FC,
∴∠GFC=∠D,FC=DC
在Rt△GDC和Rt△GEC中,$\left\{\begin{array}{l}{FC=DC}\\{CG=CG}\end{array}\right.$,
∴Rt△GFC≌Rt△GDC(HL).
∴GF=GD.
(3)在Rt△AEG中,AG=10-x,AE=10-y,GE=x+y,
由勾股定理可知:AG2+AE2=GE2,即:(10-x)2+(10-y)2=(x+y)2,
∴y=$\frac{100-10x}{10+x}$.
点评 本题主要考查的是翻折的性质、正方形的性质、勾股定理、平行线的性质的综合应用,利用翻折的性质和正方形的性质找出相等的边和角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
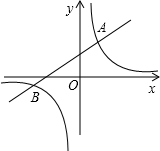 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)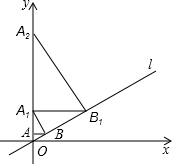 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).
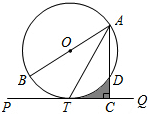 如图,AB是⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
如图,AB是⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C. 
 已知△ABC,求作△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).
已知△ABC,求作△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).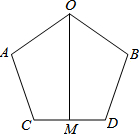 已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.
已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.