题目内容
求满足方程|a-b|+ab=1的非负整数a,b的值.分析:由方程|a-b|+ab=1的非负整数a,b这一条件,可知ab≥0,所以ab=0或ab=1,进一步解出方程组即可.
解答:解:由于a,b为非负整数,
所以
或
解得:
或
或
.
所以
|
|
解得:
|
|
|
点评:此题主要考查了绝对值的意义,以及二元一次方程组的解法,题目比较简单,但很典型.

练习册系列答案
相关题目
 ,方差
,方差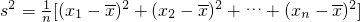 .
.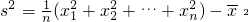 ;并且s2≥0,当x1=x2=…=xn=
;并且s2≥0,当x1=x2=…=xn=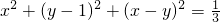 的一切实数对(x,y).
的一切实数对(x,y).