题目内容
设一组数据是x1,x2,…,xn,它们的平均数是. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
(Ⅰ)证明:方差也可表示为s2=
| 1 |
| n |
| x | 2 1 |
| x | 2 2 |
| x | 2 n |
. |
| x |
. |
| x |
(Ⅱ)求满足方程x2+(y-1)2+(x-y)2=
| 1 |
| 3 |
分析:(1)根据方差的定义的公式展开,进行整理得出命题的正确性;
(2)结合方差s2=
[x2+(y-1)2+(x-y)2]-(
)2=
-(-
)2,当且仅当-x=y-1=x-y=
=-
时,求出即可.
(2)结合方差s2=
| 1 |
| 3 |
. |
| a |
| 1 |
| 9 |
| 1 |
| 3 |
. |
| a |
| 1 |
| 3 |
解答:解:(1)∵s2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],
=
[x12+(
) 2-2x1
+x22+(
) 2-2x2
+…+xn2+(
) 2-2xn
],
=
(x12+x22+…+xn2)+
((
) 2+(
) 2+…+(
) 2)+
(-2x1
-2x2
-…-2xn
],
=
(x12+x22+…+xn2)+(
) 2+
(-2x1
-2x2
-…-2xn
],
=
(x12+x22+…+xn2)+(
) 2-2
(x1+x2+…+xn],
=
(x12+x22+…+xn2)-(
) 2,
∴s2=
(
+
+…+
)-
2;
当x1=x2=…=xn=
时,
s2=(
) 2-(
) 2=0,
∴此时方差s2取最小值0;
(2)设数据-x,(y-1),x-y的平均数为:
=
[(-x)+(y-1)+(x-y)],
=-
,
方差s2=
[x2+(y-1)2+(x-y)2]-(
)2=
-(-
)2,
当且仅当-x=y-1=x-y=
=-
时,
s2=0,
此时x=
,y=
.
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
. |
| x |
| 1 |
| n |
=
| 1 |
| n |
. |
| x |
∴s2=
| 1 |
| n |
| x | 2 1 |
| x | 2 2 |
| x | 2 n |
. |
| x |
当x1=x2=…=xn=
. |
| x |
s2=(
. |
| x |
. |
| x |
∴此时方差s2取最小值0;
(2)设数据-x,(y-1),x-y的平均数为:
. |
| a |
| 1 |
| 3 |
=-
| 1 |
| 3 |
方差s2=
| 1 |
| 3 |
. |
| a |
| 1 |
| 9 |
| 1 |
| 3 |
当且仅当-x=y-1=x-y=
. |
| a |
| 1 |
| 3 |
s2=0,
此时x=
| 1 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了方差公式的证明以及综合应用,正确的将公式变形是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,方差
,方差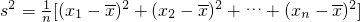 .
.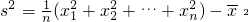 ;并且s2≥0,当x1=x2=…=xn=
;并且s2≥0,当x1=x2=…=xn=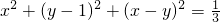 的一切实数对(x,y).
的一切实数对(x,y). ,方差
,方差 .
. ;并且s2≥0,当x1=x2=…=xn=
;并且s2≥0,当x1=x2=…=xn=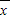 时,方差s2取最小值0;
时,方差s2取最小值0; 的一切实数对(x,y).
的一切实数对(x,y).