题目内容
18.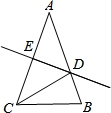 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.(1)若∠A=40°,则∠DCB=30°.
(2)若AE=4,△DCB的周长为13,则BC=5.
分析 先根据AB=AC求出∠ABC的度数,再根据线段垂直平分线的性质求出∠ACD的度数,进而可求出∠DCB的度数;根据线段垂直平分线的性质求出CD=AD,再通过等量代换即可求出结论.
解答 解:∵AB=AC,∠A=40°,
∴∠ABC=$\frac{180°-∠A}{2}$=70°,
∵D是线段AB垂直平分线上的点,
∴∠ACD=∠A=40°,
∴∠DCB=∠ABC-∠ABD=70°-40°=30°;
∵D是线段AB垂直平分线上的点,
∴AE=CE=4,AD=CD,
∴AD+BD=BD+CD=AB=8,
∵△DCB的周长为13,
∴BD+CD+BC=AB+BC=13,
∴BC=5,
故答案为:30°,5.
点评 本题考查了线段垂直平分线的性质,等腰三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
3.下列说法不正确的是( )
| A. | 两对应角相等的三角形是相似三角形 | |
| B. | 两对应边成比例的三角形是相似三角形 | |
| C. | 三边对应成比例的三角形是相似三角形 | |
| D. | 以上有两个说法是正确 |
10.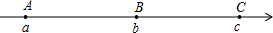 如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
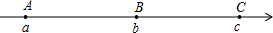 如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )| A. | 点A与点B之间靠近A点 | B. | 点A与点B之间靠近A点或点A的左边 | ||
| C. | 点B与点C之间靠近C点 | D. | 点B与点C之间靠近C点或点C的右边 |
 如图,△OCA≌△OBD,则这两个三角形中相等的边有AC=BD,OC=OB,OA=OD,相等的角有∠A=∠D,∠C=∠B,∠AOC=∠DOB.
如图,△OCA≌△OBD,则这两个三角形中相等的边有AC=BD,OC=OB,OA=OD,相等的角有∠A=∠D,∠C=∠B,∠AOC=∠DOB.