题目内容
4.已知,点D是△ABC内一点,满足AD=AC(1)已知∠CAD=2∠BAD,∠ABD=30°,如图1,若∠BAC=60°,∠ACB=80°,请判断BD和CD的数量关系(直接写出答案)
(2)如图2,若∠ACB=2∠ABC,BD=CD,试证明∠CAD=2∠BAD.
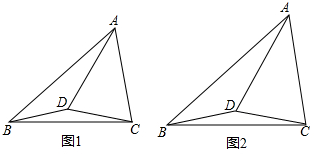
分析 (1)根据三角形内角和定理求得∠ABC=40°,进一步求得∠BAD=20°,∠ADC=∠ACD=70°,从而求得∠DBC=∠ABC-∠ABD=40°-30°=10°,∠DCB=∠ACB-∠ACD=80°-70°=10°,得出∠DBC=∠DCB,证得DB=DC;
(2)作∠EBC=∠ACB,使EB=AC,连接ED、EA,则四边形AEBC是等腰梯形,通过证得△EBD≌△ACD得出ED=AD,进一步证得三角形AED是等边三角形,可得∠EAD=60°,然后根据∠BAD=60°-∠EAB=60°-∠ABC,利用等量代换即可证得结论.
解答 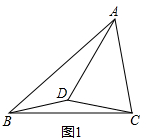 解:(1)BD和CD的数量关系是BD=CD;
解:(1)BD和CD的数量关系是BD=CD;
理由:∵在△ABC中,∠BAC=60°,∠ACB=80°,
∴∠ABC=40°,
∵∠CAD=2∠BAD,
∴∠CAD=40°,∠BAD=20°,
又∵AD=AC,
∴∠ADC=∠ACD=70°,
∴∠DBC=∠ABC-∠ABD=40°-30°=10°,∠DCB=∠ACB-∠ACD=80°-70°=10°,
∴∠DBC=∠DCB,
∴DB=DC;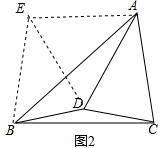
(2)作∠EBC=∠ACB,使EB=AC,连接ED、EA,则四边形AEBC是等腰梯形,
∴AE∥BC,
∴∠EAB=∠ABC,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠EBD=∠ACD,
在△EBD和△ACD中
$\left\{\begin{array}{l}{BE=AC}\\{∠EBD=∠ACD}\\{BD=CD}\end{array}\right.$
∴△EBD≌△ACD(SAS),
∴ED=AD,
∵∠ACB=2∠ABC,∠EBC=∠ACB,
∴∠EBC=2∠ABC,
∴∠ABE=∠ABC,
∴∠EAB=∠ABE,
∴BE=AE,
∵AD=AC=EB,
∴EA=ED=AD,
∴△AED是等边三角形,
∴∠EAD=60°,
∴∠BAD=60°-∠EAB=60°-∠ABC,
∴2∠BAD=120°-2∠ABC=120°-∠ACB,
∵AE∥BC,
∴∠ACB+∠EAC=180°,
∴∠ACB=180°-∠EAC,
∵∠EAC=60°+∠DAC,
∴2∠BAD=120°-(180°-60°-∠DAC)=∠DAC,
∴∠DAC=2∠BAD.
点评 题主要考查了等腰三角形的性质、等边三角形的判定和性质、全等三角形的判定与性质,作辅助线构建等腰梯形,通过证明三角形全等得出线段相等,是解答本题的基本思路.

 阅读快车系列答案
阅读快车系列答案| A. | 4.25×109 | B. | 4.25×1010 | C. | 4.25×1011 | D. | 4.25×1012 |
| A. | 如果两个角相等,那么这两个角是对顶角 | |
| B. | 直线外一点和直线上的点连线,垂线最短 | |
| C. | 平面内经过一点有且只有一条直线与已知直线平行 | |
| D. | 平面内经过一点有且只有一条直线与已知直线垂直 |
| A. | 90×104 | B. | 9×104 | C. | 9×105 | D. | 0.9×105 |
| A. | 周长相等的两个三角形全等 | |
| B. | 关于某条直线对称的两个三角形全等 | |
| C. | 顶角相等的两个等腰三角形全等 | |
| D. | 两边和一角对应相等的两个三角形全等 |