题目内容
△ABC中，BE⊥AC，CF⊥AB，垂足分别为E、F，M、N分别是BC、EF的中点，求证。MN⊥EF。
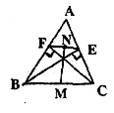
证明：连接FM，EM
∵CF⊥AB，BE⊥AC
∴∠CFB=∠BEC=90°
Rt△CFB与Rt△CEB中
∵M是BC的中点
∴MF=
BC，ME=BC
∴MF=ME
又∵N是EF的中点
∴MN⊥EF
练习册系列答案
相关题目
题目内容
△ABC中，BE⊥AC，CF⊥AB，垂足分别为E、F，M、N分别是BC、EF的中点，求证。MN⊥EF。
证明：连接FM，EM
∵CF⊥AB，BE⊥AC
∴∠CFB=∠BEC=90°
Rt△CFB与Rt△CEB中
∵M是BC的中点
∴MF=BC，ME=BC
∴MF=ME
又∵N是EF的中点
∴MN⊥EF
已知：如图，在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连AD、AG．求证：AG=AD．
知识链接：三角形三个内角的和是180度．（如图∠A是△ABC的一个内角）如图：△ABC中，BE、CF分别是∠ABC和∠ACB的平分线，BE、CF相交于点O．
（2013•徐汇区一模）如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．