Question

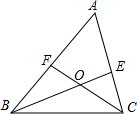知识链接：三角形三个内角的和是180度．（如图∠A是△ABC的一个内角）如图：△ABC中，BE、CF分别是∠ABC和∠ACB的平分线，BE、CF相交于点O．
（1）如果∠A=40度，求∠BOC的度数；
（2）如果∠A=50度，直接写出∠BOC的度数；
（3）探求∠A和∠BOC的关系（用等式表示），并简要说明理由．

Answer 1

分析：（1）先根据三角形内角和定理求出∠ABC+∠ACB的度数，再根据角平分线的性质可求出∠EBC+∠FCB的度数，再由三角形的内角和为180°即可解答；
（2）同（1），根据三角形的内角和定理及角平分线的性质解答即可；
（3）根据（1）的叙述写出结论即可．

解答：解：（1）∵∠A+∠ABC+∠ACB=180°，∠A=40°，
∴∠ABC+∠ACB=180°-∠A=140°，
∵∠EBC=

1

2

∠ABC∠FCB=

1

2

∠ACB，
∴∠EBC+∠FCB=

1

2

（∠ABC+∠ACB）=70°，
∴∠BOC=180°-70°=110°；

（2）同（1）∠BOC=180°-

180°-∠A

2

=180°-

180°-50°

2

=115°；

（3）由（1）可知：∠BOC=90°+

1

2

∠A，
理由同（1），∵∠A+∠ABC+∠ACB=180°，BE、CF分别是∠ABC、∠ACB的平分线，
∴∠OBC=

1

2

∠ABC，∠OCB=

1

2

∠ACB，
∴∠OBC+∠OCB=

1

2

（∠ABC+∠ACB），
∴∠OBC+∠OCB=

1

2

（180°-∠A）=90°-

1

2

∠A，
∵∠BOC+∠OBC+∠OCB=180°，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-90°+

1

2

∠A=90°+

1

2

∠A．

点评：本题考查的是三角形内角和定理及角平分线的性质，比较简单．