Question

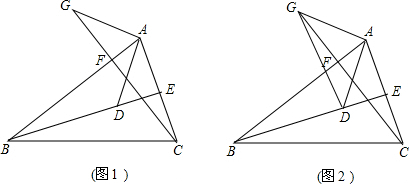
如图1，在△ABC中，BE、CF分别是AC、AB两边上的高，D在BE上，且BD=AC，G在CF的延长线上且取CG=AB，连接AD，AG．  
（1）求证：△ABD≌△GCA；
（2）如图2，若条件不变，连接GD，那么△ADG的形状是

等腰直角三角形

．（只填结论即可）

Answer 1

分析：（1）根据三角形高线的定义得到∠BEA=∠CFA=90°，再根据等角的余角相等得到∠ABE=∠ACF，然后根据“SAS”可判断△ABD≌△GCA；
（2）根据△ABD≌△GCA得到AD=AG，∠AGC=∠BAD，由于∠AGC+∠GAF=90°，则∠GAF+∠BAD=90°，即可判断△ADG为等腰直角三角形．

解答：（1）证明：∵BE、CF分别是AC、AB两边上的高，
∴∠BEA=∠CFA=90°，
∴∠ABE+∠BAC=90°，∠ACF+∠BAC=90°，
∴∠ABE=∠ACF，
在△ABD和△GCA中

BD=AC ∠ABE=∠ACF AB=CG

，
∴△ABD≌△GCA（SAS）；

（2）解：∵△ABD≌△GCA，
∴AD=AG，∠AGC=∠BAD，
而∠AGC+∠GAF=90°，
∴∠GAF+∠BAD=90°，
即∠GAD=90°，
∴△ADG为等腰直角三角形．
故答案为等腰直角三角形．

点评：本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了等腰直角三角形的判定．