题目内容
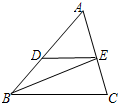（2013•徐汇区一模）如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．（1）求证：AE•BC=BD•AC；
（2）如果S△ADE=3，S△BDE=2，DE=6，求BC的长．
分析：（1）由BE平分∠ABC交AC于点E，ED∥BC，可证得BD=DE，△ADE∽△ABC，然后由相似三角形的对应边成比例，证得AE•BC=BD•AC；
（2）根据三角形面积公式与S△ADE=3，S△BDE=2，可得AD：BD=3：2，然后由平行线分线段成比例定理，求得BC的长．
（2）根据三角形面积公式与S△ADE=3，S△BDE=2，可得AD：BD=3：2，然后由平行线分线段成比例定理，求得BC的长．
解答：（1）证明：∵BE平分∠ABC，
∴∠ABE=∠CBE．…（1分）
∵DE∥BC，
∴∠DEB=∠CBE…（1分）
∴∠ABE=∠DEB．
∴BD=DE，…（1分）
∵DE∥BC，
∴△ADE∽△ABC，
∴
=
…（1分）
∴
=
，
∴AE•BC=BD•AC；…（1分）
（2）解：设△ABE中边AB上的高为h．
∴
=
=
=
，…（2分）
∵DE∥BC，
∴
=
． …（1分）
∴
=
，
∴BC=10． …（2分）
∴∠ABE=∠CBE．…（1分）
∵DE∥BC，
∴∠DEB=∠CBE…（1分）
∴∠ABE=∠DEB．
∴BD=DE，…（1分）
∵DE∥BC，
∴△ADE∽△ABC，
∴
| AE |
| AC |
| DE |
| BC |
∴
| AE |
| AC |
| BD |
| BC |
∴AE•BC=BD•AC；…（1分）
（2）解：设△ABE中边AB上的高为h．
∴
| S△ADE |
| S△BDE |
| ||
|
| AD |
| BD |
| 3 |
| 2 |
∵DE∥BC，
∴
| DE |
| BC |
| AD |
| AB |
∴
| 6 |
| BC |
| 3 |
| 5 |
∴BC=10． …（2分）
点评：此题考查了相似三角形的判定与性质、平行线分线段成比例定理以及等腰三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
（2013•徐汇区一模）“数学迷”小楠通过从“特殊到一般”的过程，对倍角三角形（一个内角是另一个内角的2倍的三角形）进行研究．得出结论：如图1，在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，如果∠A=2∠B，那么a2-b2=bc．