题目内容
7.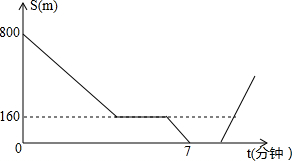 在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.
在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.
分析 根据速度=路程÷时间,可求出队伍的速度,根据通讯员的速度=800÷追上队首的时间(去掉传达命令的两分钟)+队伍的速度,可求出通讯员的速度,再用队伍的长度÷二者的速度和+7+2,即可求出通讯员回到队尾的时间,由路程=通讯员的速度×追赶及返回的时间(不包括两次传达命令的时间)+队伍的速度×两次传达命令的时间,即可求出通讯员走过的总路程.
解答 解:队伍的速度为800÷10=80(米/分钟),
通讯员的速度为800÷(7-2)+80=240(米/分钟),
通讯员回到队尾的时间为7+2+160÷(80+240)=$\frac{19}{2}$(分钟),
通讯员走的总路程为($\frac{19}{2}$-4)×240+4×60=1560(米).
故答案为:1560.
点评 本题考查了一次函数的应用,观察函数图象找出各数据,再根据数量关系列式计算是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列命题中,真命题的个数是( )
①两条直线被第三条直线所截,同位角相等
②经过直线外一点,有且只有一条直线与这条直线平行
③同旁内角相等,两直线平行
④负数没有立方根.
①两条直线被第三条直线所截,同位角相等
②经过直线外一点,有且只有一条直线与这条直线平行
③同旁内角相等,两直线平行
④负数没有立方根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若am=2,an=4,则am+n等于( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
19.下列等式恒成立的是( )
| A. | (m+n)(-m-n)=m2-n2 | B. | (2a-b)2=4a2-2ab+b2 | ||
| C. | (x+3)(-x+3)=x2-9 | D. | (4x+1)2=16x2+8x+1 |
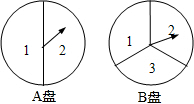 小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由. 如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )