题目内容
9.某装修店里出售下列形状的地砖:(1)正三角形;(2)正方形;(3)正六边形;(4)正八边形,若只选购一种地砖来铺满地面,则购买方案共有3种.分析 由镶嵌的条件知,判断一种图形是否能够镶嵌,只要看一看正多边形的内角度数是否能整除360°,能整除的可以平面镶嵌,反之则不能.
解答 解:①正三角形的每个内角是60°,能整除360°,6个能组成镶嵌
②正方形的每个内角是90°,4个能组成镶嵌;
③正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
④正八边形每个内角是180°-360°÷8=135°,不能整除360°,不能密铺;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有3种.
故答案为:3.
点评 此题主要考查了平面镶嵌,用一种正多边形的镶嵌应符合一个内角度数能整除360°.任意多边形能进行镶嵌,说明它的内角和应能整除360°.

练习册系列答案
相关题目
4.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
那么这50名学生平均每人植树4棵.
| 植树棵数 | 3 | 4 | 5 | 6 |
| 人数 | 20 | 15 | 10 | 5 |
14.要反映一个家庭在教育方面支出占总收入的比,宜采用( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布直方图 |
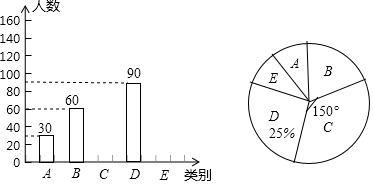
18.空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )
| A. | 折线图 | B. | 条形图 | C. | 直方图 | D. | 扇形图 |
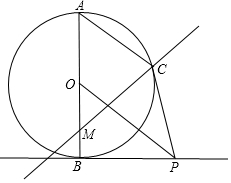 已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP,M是直径AB上的动点,A与直线CM上的点连线距离的最小值为d,B与直线CM上的点连线距离的最小值为f.
已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP,M是直径AB上的动点,A与直线CM上的点连线距离的最小值为d,B与直线CM上的点连线距离的最小值为f.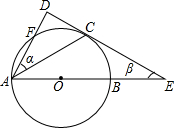 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.
如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.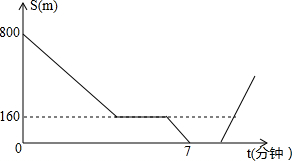 在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.
在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.