题目内容
 在△ABC中,AD是BC边上的高,BC=12,AD=8.矩形EFGH的顶点E、F分别在AB、AC上,H、G在BC上.
在△ABC中,AD是BC边上的高,BC=12,AD=8.矩形EFGH的顶点E、F分别在AB、AC上,H、G在BC上.(1)当EF=
(2)求矩形EFGH的最大面积.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)设HG=x,KD=y,根据矩形的对边平行可得HG∥EF,然后得到△AEF与△ABC相似,根据相似三角形对应高的比等于相似比列出比例式,用x表示出y,当x=y时,矩形EFGH是正方形,求出x的值;
(2)根据矩形的面积公式求解并整理,再利用二次函数的最值问题进行求解即可.
(2)根据矩形的面积公式求解并整理,再利用二次函数的最值问题进行求解即可.
解答:解:(1)设EF=x,KD=y,
∵四边形EFGH是矩形,
∴HG∥EF,
∴△AEF∽△ABC,
∵AD是BC边上的高,
∴AK⊥HG,∠ADG=∠HGF=∠GFK=90°,
∴四边形DGFK是矩形,
∴KD=GF=y,
∴AK:AD=EF:BC,
∵BC=12,AD=8,
∴
=
,
∴y=-
x+8,
当x=y时,矩形EFGH是正方形,
∴x=-
x+8,解得x=
,
即EF=
时,矩形EFGH是正方形;
(2)∵矩形EFGH的面积为:xy=x(-
x+8)=-
(x-6)2+24,∵-
<0,
∴当x=6,即EF=6时,内接矩形EFGH有最大面积,最大面积是24.
∵四边形EFGH是矩形,
∴HG∥EF,
∴△AEF∽△ABC,
∵AD是BC边上的高,
∴AK⊥HG,∠ADG=∠HGF=∠GFK=90°,
∴四边形DGFK是矩形,
∴KD=GF=y,
∴AK:AD=EF:BC,
∵BC=12,AD=8,
∴
| 8-y |
| 8 |
| x |
| 12 |
∴y=-
| 2 |
| 3 |
当x=y时,矩形EFGH是正方形,
∴x=-
| 2 |
| 3 |
| 24 |
| 5 |
即EF=
| 24 |
| 5 |
(2)∵矩形EFGH的面积为:xy=x(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴当x=6,即EF=6时,内接矩形EFGH有最大面积,最大面积是24.
点评:本题考查了矩形的性质、相似三角形的判定与性质以及二次函数的最值问题;根据相似三角形对应高的比等于相似比列出比例式求出矩形长与宽的关系是解题关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
如果n边形的内角和等于外角和的3倍,那么n的值是( )
| A、5 | B、6 | C、7 | D、8 |
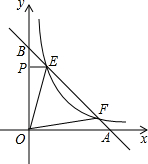 如图,点E,F在函数y=
如图,点E,F在函数y=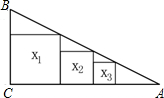 如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题:
如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题: 在Rt△ABC中,∠C=90°,b=5,c=5
在Rt△ABC中,∠C=90°,b=5,c=5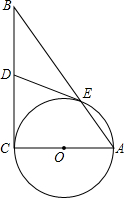 如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,
如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,