题目内容
14.如图,已知AB是⊙O的直径,CD是半圆上两点.AB=26,AC=10(1)若点D是$\widehat{AB}$的中点,求AD的长;
(2)若点D是$\widehat{BC}$中点,求AD长.
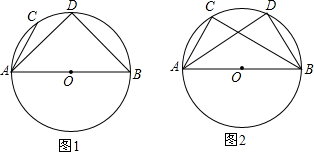
分析 (1)由点D是$\widehat{AB}$的中点,AB是⊙O的直径,易证得△ABD是等腰直角三角形,又由AB=26,即可求得AD的长;
(2)首先连接OD,由点D是$\widehat{BC}$中点,可得OD垂直平分BC,然后由勾股定理求得BC的长,由三角形中位线的性质,求得OE的长,继而求得DE,BD,再由勾股定理,求得AD长.
解答 解:(1)∵AB是⊙O的直径,
∴∠D=90°,
∵点D是$\widehat{AB}$的中点,
∴AD=BD,
∴△ABD是等腰直角三角形,
∵AB=26,
∴AD=AB•cos45°=26×$\frac{\sqrt{2}}{2}$=13$\sqrt{2}$;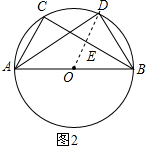 (2)连接OD交BC于E点,
(2)连接OD交BC于E点,
∵AB为直径,
∴AC⊥BC,
又∵AB=26,AC=10,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=24,
∵点D是$\widehat{BC}$中点,
∴OD垂直平分BC,由此可得:OE=$\frac{1}{2}$AC=5,
∴DE=OD-OE=13-5=8,
又∵BE=$\frac{1}{2}$BC=12,
在Rt△BDE中,由勾股定理,得BD2=BE2+DE2=208,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{2{6}^{2}-208}$=12$\sqrt{13}$.
点评 此题考查了圆周角定理、垂径定理以及勾股定理.注意掌握辅助线的作法.

练习册系列答案
相关题目
 如图,已知AB=DC,BE=CF,只需再补充∠B=∠C或AB∥CD,就可以证明△ABE≌△DCF.
如图,已知AB=DC,BE=CF,只需再补充∠B=∠C或AB∥CD,就可以证明△ABE≌△DCF.