题目内容
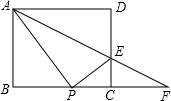 如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.
如图,在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,设BP=a.(1)当点P在线段BC上时(点P与点B,C都不重合),试用含a的代数式表示CE;
(2)当a=3时,连结DF,试判断四边形APFD的形状,并说明理由;
(3)当tan∠PAE=
| 1 |
| 2 |
考点:四边形综合题
专题:几何综合题,数形结合
分析:(1)PC在BC上运动时,只需要用勾股定理表示PE2=PC2+EC2就可以使问题到解决,而关键是解决PE2,又在Rt△APE中由勾股定理求得,从而解决问题.
(2)把a=3的值代入第一问的解析式就可以求出CE的值,再利用三角形相似就可以求出CF的值.
(3)由条件可以证明△ABP∽△PCE,可以得到
=
=2,再分情况讨论,从而求出a的值.
(2)把a=3的值代入第一问的解析式就可以求出CE的值,再利用三角形相似就可以求出CF的值.
(3)由条件可以证明△ABP∽△PCE,可以得到
| BP |
| CE |
| AB |
| PC |
解答: 解:(1)如图1,∵四边形ABCD是矩形,
解:(1)如图1,∵四边形ABCD是矩形,
∴AB=CD=4,BC=AD=5,∠B=∠BCD=∠D=90°,
∵BP=a,
∴PC=5-a,DE=4-CE,
∵AP⊥PE,
∴∠APE=90°,∠1+∠2=90°,
∵∠1+∠3=90°,
∴∠2=∠3,
∴△ABP∽△PCE,
∴
=
,
∴
=
,
∴EC=
,
自变量的取值范围为:0<a<5;
(2)当a=3时,EC=
=
,
∴DE=
,
∵四边形ABCD是矩形,
∴AD平行于BF.
∴△AED∽△FEC,
∴
=
,
∴
=
,
∴CF=3,
∴PF=AD=5,
∴四边形APFD是平行四边形;
(3)如图2,根据tan∠PAE=
,可得:
=2,
∵∠APB+∠BPE=90°,∠CEP+∠EPC=90°,
∴∠CEP=∠APB,
又∵∠ABP=∠PCE,
∴△ABP∽△PCE
∴
=
=2
于是:
=
=2 ①或
=
=2 ②
解得:a=3,EC=1.5或 a=7,EC=3.5.
∴a=3或7.
 解:(1)如图1,∵四边形ABCD是矩形,
解:(1)如图1,∵四边形ABCD是矩形,∴AB=CD=4,BC=AD=5,∠B=∠BCD=∠D=90°,
∵BP=a,
∴PC=5-a,DE=4-CE,
∵AP⊥PE,
∴∠APE=90°,∠1+∠2=90°,
∵∠1+∠3=90°,
∴∠2=∠3,
∴△ABP∽△PCE,
∴
| CE |
| BP |
| PC |
| AB |
∴
| CE |
| a |
| 5-a |
| 4 |
∴EC=
| -a2+5a |
| 4 |
自变量的取值范围为:0<a<5;
(2)当a=3时,EC=
| -32+5×3 |
| 4 |
| 3 |
| 2 |
∴DE=
| 5 |
| 2 |
∵四边形ABCD是矩形,
∴AD平行于BF.
∴△AED∽△FEC,

∴
| AD |
| CF |
| DE |
| CE |
∴
| 5 |
| CF |
| ||
|
∴CF=3,
∴PF=AD=5,
∴四边形APFD是平行四边形;
(3)如图2,根据tan∠PAE=
| 1 |
| 2 |
| AP |
| PE |
∵∠APB+∠BPE=90°,∠CEP+∠EPC=90°,
∴∠CEP=∠APB,
又∵∠ABP=∠PCE,
∴△ABP∽△PCE
∴
| BP |
| CE |
| AB |
| PC |
于是:
| a |
| EC |
| 4 |
| 5-a |
| a |
| EC |
| 4 |
| a-5 |
解得:a=3,EC=1.5或 a=7,EC=3.5.
∴a=3或7.
点评:本题考查了相似三角形的判定与性质,矩形的性质,解直角三角形以及勾股定理的运用,利用数形结合得出是解题关键.

练习册系列答案
相关题目
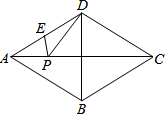 已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是
已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是