题目内容
求抛物线y=-
x2与直线y=2x-3的交点坐标.
| 2 |
| 3 |
考点:二次函数的性质
专题:
分析:联立两解析式解方程组即可求得两函数图象的交点坐标.
解答:解:
联立两函数的解析式可得
,
解这个方程组得
或
,
所以抛物线y=-
x2与直线y=2x-3的交点坐标为(-
+
,-6+3
)和(-
-
,-6-3
).
联立两函数的解析式可得
|
解这个方程组得
|
|
所以抛物线y=-
| 2 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 2 |
点评:本题主要考查函数图象交点的计算,掌握求函数图象的交点的方法,即联立解析式得到方程组,求方程组的解是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,在?ABCD中,EF∥AB,FG∥ED,DE:EA=2:3,EF=4,求线段CG的长.
如图,在?ABCD中,EF∥AB,FG∥ED,DE:EA=2:3,EF=4,求线段CG的长.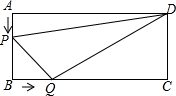 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P点P从A出发沿边AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿边BC以2cm/s的速度向点C移动,(P、Q两点同时停止运动)几秒钟后△PBQ的面积等于28cm2?
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P点P从A出发沿边AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿边BC以2cm/s的速度向点C移动,(P、Q两点同时停止运动)几秒钟后△PBQ的面积等于28cm2?