题目内容
12.有一个材质为白色的正方体表面涂成绿色,再分割成同样大小的27个小正方体,从这些小正方体中任取一个,恰有两个面涂成绿色的概率是$\frac{4}{9}$.分析 将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体,可得基本事件的总数有27个,然后计算出满足条件恰有两面涂有颜色的基本事件个数,代入古典概型概率公式即可得到答案.
解答 解:一块各面均涂有油漆的正方体被锯成27个同样大小的小正方体,
其中满足两面漆有油漆的小正方体有12个
故从中随机地取出一个小正方体,其两面漆有油漆的概率P=$\frac{12}{27}$=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题考查的知识点是古典概型及其概率计算公式,其中根据棱柱的结构特征,根据正方体共有12条棱,计算出两面漆有颜色的基本事件个数,是解答本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
2.已知一次函数y=(m-3)x+m-4的图象不经过第二象限,则m的取值范围是( )
| A. | m>3 | B. | m>4 | C. | 3<m<4 | D. | 3<m≤4 |
7.已知a-b=3,ab=2,则a2+b2的值是( )
| A. | 3 | B. | 13 | C. | 9 | D. | 11 |
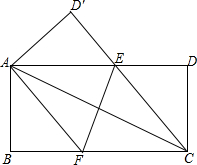 如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处
如图,在一张矩形纸片中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C恰好与点A重合,点D落在点D′处