题目内容
14.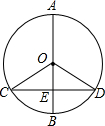 如图所示,⊙O的直径AB垂直于弦CD,AB,CD相交于点E,$\widehat{AD}$的度数为130°,则∠COD=100°.
如图所示,⊙O的直径AB垂直于弦CD,AB,CD相交于点E,$\widehat{AD}$的度数为130°,则∠COD=100°.
分析 根据垂径定理和圆心角定理即可得到结果.
解答 解:∵⊙O的直径AB垂直于弦CD,
∴$\widehat{AC}=\widehat{AD}$,
∴∠AOC=∠AOD,
∵$\widehat{AD}$的度数为130°,
∴∠AOC=∠AO=130°,
∴∠COD=360°-130°-130°=100°,
故答案为;100°
点评 本题考查了圆心角、弧、弦的关系,垂径定理,熟练掌握垂径定理是解题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
4.下列各式中,y随x的变化关系式是正比例函数的是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=x-1 | D. | y=x2-1 |
5.点A(-3,-5)向左平移3个单位,再向上平移4个单位到点B,则点B的坐标在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.在下列图形中,正确画出△ABC的AC边上的高的图形是( )
| A. | 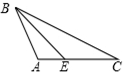 | B. | 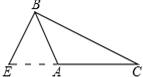 | C. | 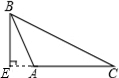 | D. |  |
